gkkleader.h File Reference

This graph shows which files directly or indirectly include this file:

Go to the source code of this file.

Functions
int	GKK_doublingtable (int x, int m, int emax, int *dt)
int	GKK_modpow (int *dt, int e, int m)
int	GKK_primroot (int p, int e, primedec_t *pr_p1, int t_p1)
int	GKK_multorder (int n, int p, int e, int pe, primedec_t *pr_p1, int t_p1)
void	GKK_prepare (int q, int n, primedec_t *pr_q, int *t, primedec_t **pr_pi1, int *t_pi1, int *gi, int *Nif, int *Kif, int *dif)
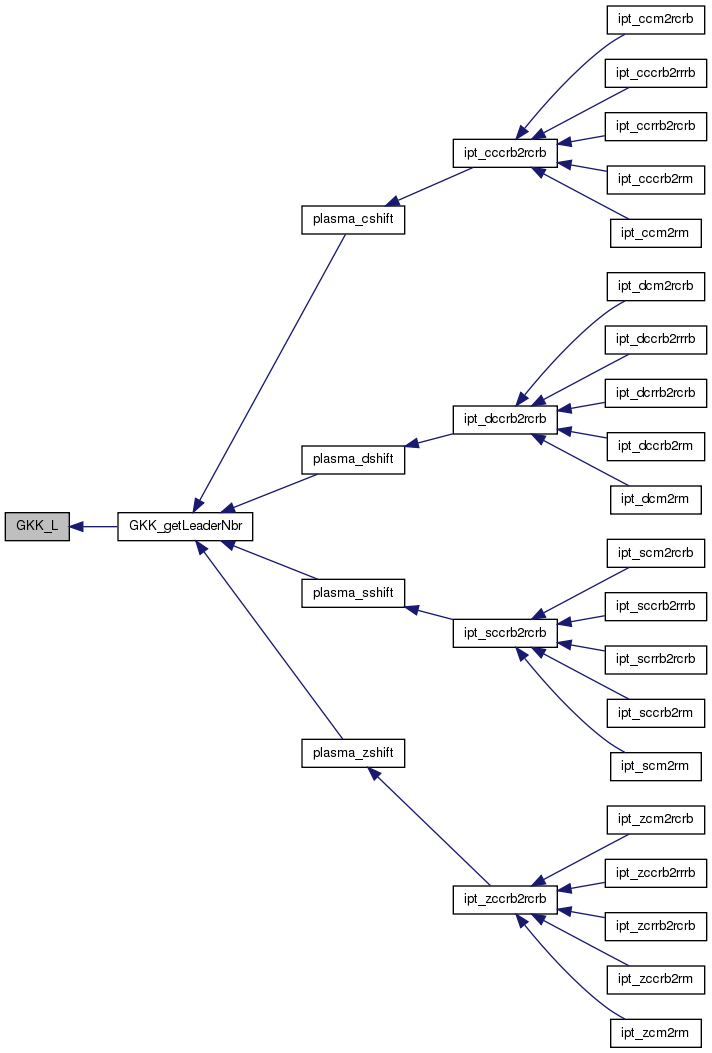
void	GKK_L (int t, primedec_t *pr_q, int *fi, int *Kif, int *dif, int *Li, int *diLi, int *cl, int *nl)
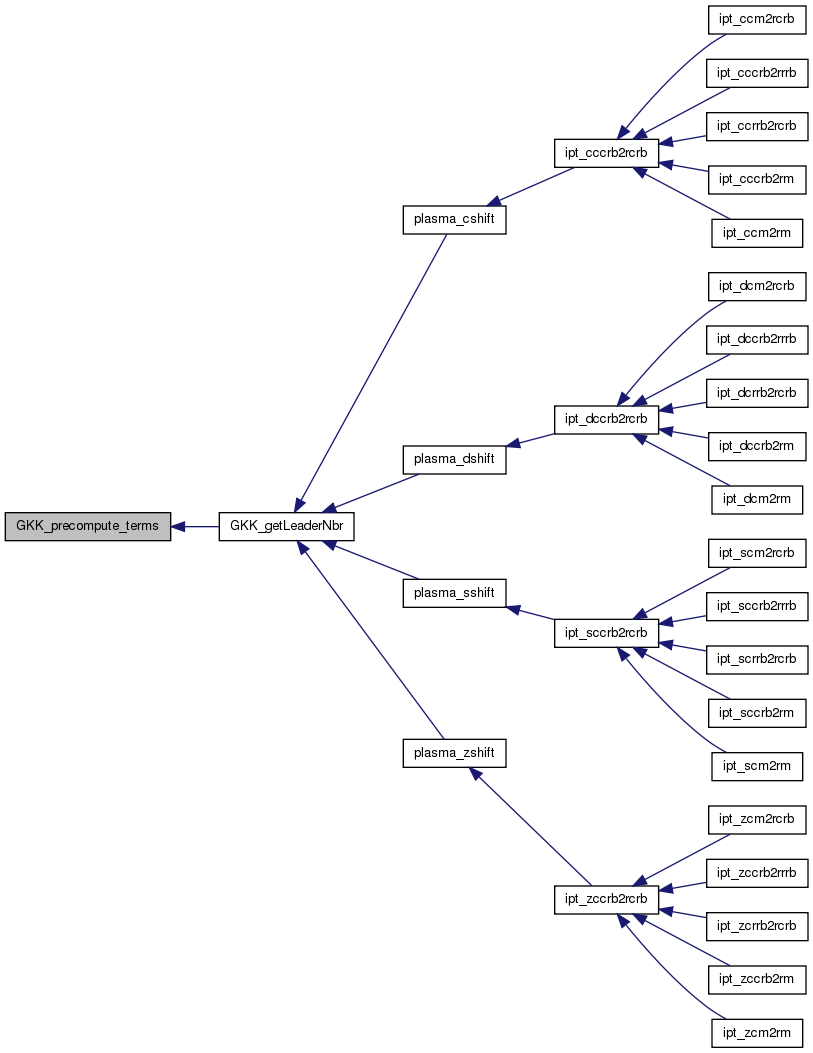
void	GKK_precompute_terms (int q, primedec_t *pr_q, int t, int *gi, int *diLi, int *rp, int *Mg, int nMg)
void	GKK_BalanceLoad (int thrdnbr, int *Tp, int *leaders, int nleaders, int L)
void	GKK_output_tables (int m, int n, int q, primedec_t *pr_q, int t, int *gi, int *Nif, int *Kif, int *dif)
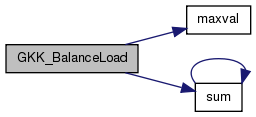
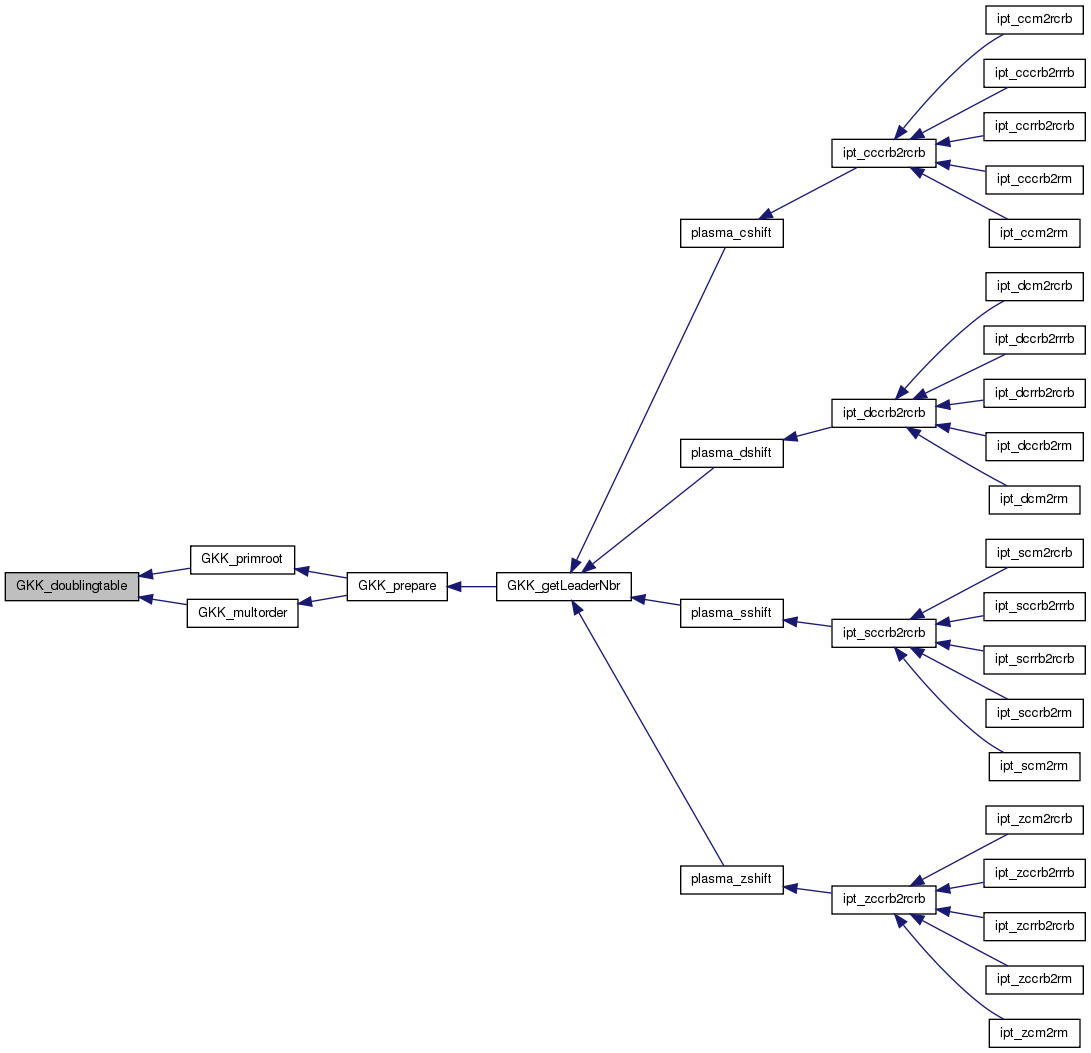
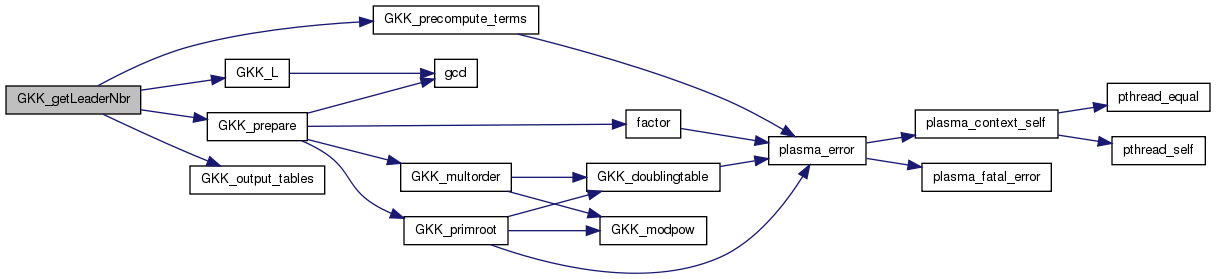
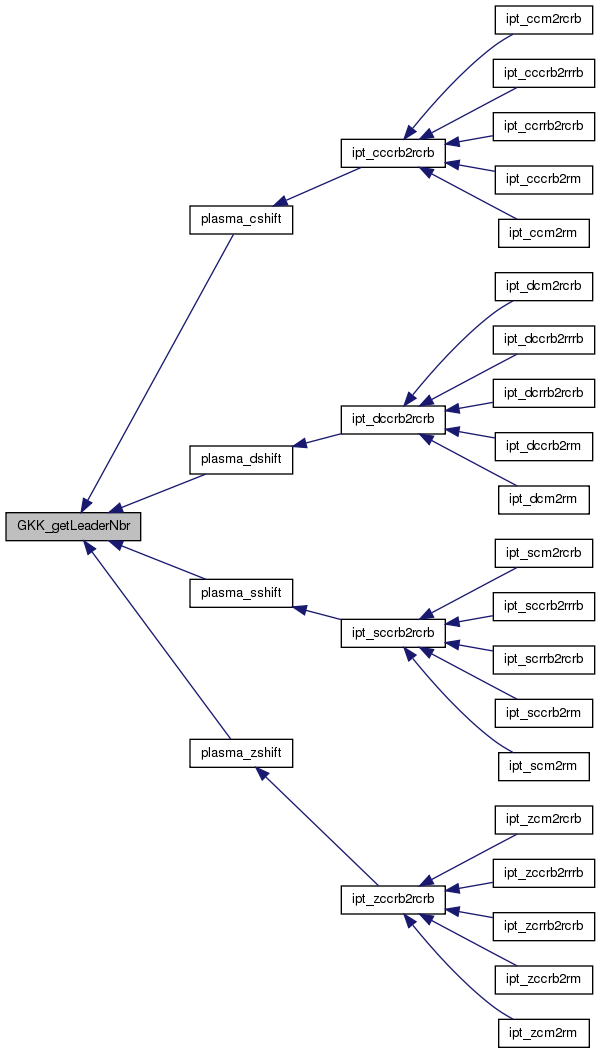
int	GKK_getLeaderNbr (int me, int ne, int *nleaders, int **leaders)

---

Detailed Description

PLASMA InPlaceTransformation module PLASMA is a software package provided by Univ. of Tennessee, Univ. of California Berkeley and Univ. of Colorado Denver

This work is the implementation of an inplace transformation based on the GKK algorithm by Gustavson, Karlsson, Kagstrom and its fortran implementation.

Version:

2.4.5

Author:

Mathieu Faverge

Date:

2010-11-15

Definition in file gkkleader.h.

---

Function Documentation

void GKK_BalanceLoad	(	int	thrdnbr,
		int *	Tp,
		int *	leaders,
		int	nleaders,
		int	L
	)

---

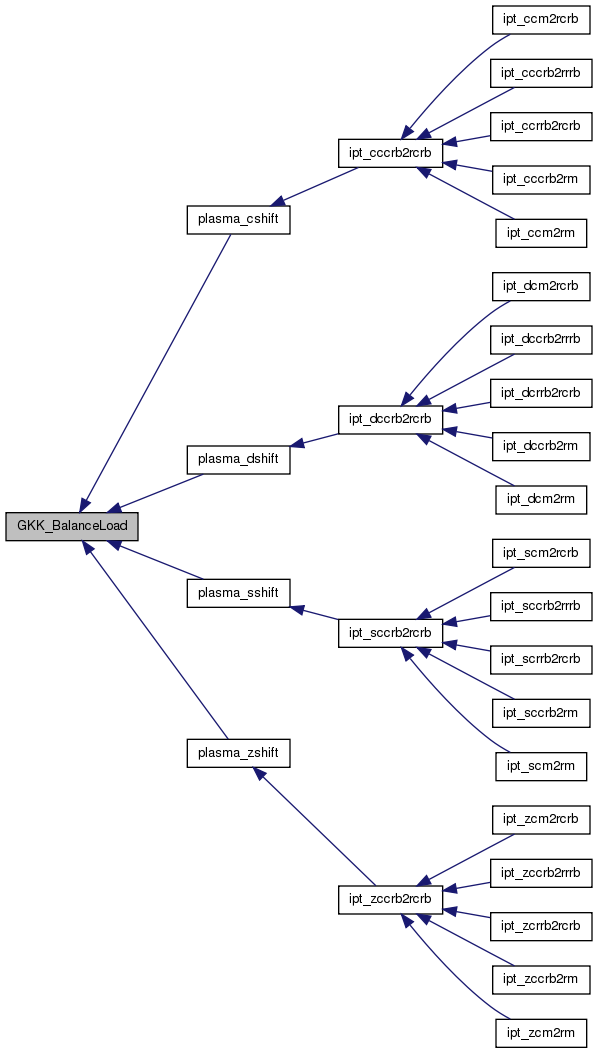
GKK_BalanceLoad balances the load by splitting across some cycles.

Parameters:

[in]	thrdnbr	number of thread working on cycles
[in,out]	Tp	Array of size thrdnbr. Work load for each thread.
[in,out]	leaders	Array of size nleaders containing leaders, cycles length and owners
[in]	nleaders	Number of leaders stored multiplied by 3
[in]	L	Chunk size to compute the load balancing

Definition at line 636 of file gkkleader.c.

References IMBALANCE_THRESHOLD, L, maxval(), min, and sum().

                                                                              {
    int    i, j, n1, nel;
    double sumTi, maxTi;

    /* quick return */
    if( thrdnbr == 1 )
        return;

    sumTi = (double)sum(thrdnbr, Tp);
    maxTi = (double)maxval(thrdnbr, Tp);
    
    /* check if the load is too imbalanced */
    if( (1.0 - (sumTi / ((double)thrdnbr * maxTi))) > IMBALANCE_THRESHOLD ) {
        /* split across cycle */
        for (i=0; i<nleaders; i+=3) {
            j   = leaders[i+2];
            nel = leaders[i+1];
            if( (nel >= thrdnbr) && 
                ((double)Tp[j] > (sumTi / ((double)thrdnbr * (1.0 - IMBALANCE_THRESHOLD)))) ) {
                /* split */
                n1 = (nel + thrdnbr - 1) / thrdnbr;
                Tp[j] = Tp[j] - nel * L;
                
                for (j=0; j<thrdnbr; j++)
                    Tp[j] = Tp[j] + min(n1, nel - n1*(j-1));

                maxTi = (double)maxval(thrdnbr, Tp);
                leaders[i+2] = -2;
            }
        }
    }
}

Here is the call graph for this function:

Here is the caller graph for this function:

int GKK_doublingtable	(	int	x,
		int	m,
		int	emax,
		int *	dt
	)

---

GKK_doublingtable Computes a table of x^i mod m for i = 1, 2, 4, 8, ..., emax

Parameters:

[in]	x
[in]	m
[in]	emax	Maximum power to compute
[out]	dt	On exit, dt contains (x^1 mod m, x^2 mod m, x^4 mod m, ..., x^emax mod m)

Definition at line 47 of file gkkleader.c.

References PLASMA_ERR_OUT_OF_RESOURCES, plasma_error(), PLASMA_SUCCESS, and PWR_MAXSIZE.

                                                       {
    int64_t y8, m8;
    int     i, numbits;
    int     z;

    /* Convert in int64 */
    m8 = m;

    /* find the number of bits in emax */
    numbits = 0;
    z = emax;
    while( z > 0 ) {
        numbits = numbits + 1;
        z = z / 2;
    }
    
    if (numbits > PWR_MAXSIZE) {
      plasma_error(__func__, "PWR_MAXSIZE too small");
      return PLASMA_ERR_OUT_OF_RESOURCES;
    }
      
    /* compute doubling table */
    y8    = x;
    dt[0] = x;
    for (i=1; i < numbits; i++){
        y8 = (y8*y8) % m8;
        dt[i] = (int)y8;
    }
    return PLASMA_SUCCESS;
}

Here is the call graph for this function:

Here is the caller graph for this function:

int GKK_getLeaderNbr	(	int	me,
		int	ne,
		int *	nleaders,
		int **	leaders
	)

Definition at line 753 of file gkkleader.c.

References primedec::e, GKK_L(), GKK_output_tables(), GKK_precompute_terms(), GKK_prepare(), primedec::p, primedec::pe, PLASMA_SUCCESS, PRIME_MAXSIZE, PWR_MAXSIZE, and SIZE_MG.

                                                                   {

    primedec_t   pr_q[PRIME_MAXSIZE];
    primedec_t **pr_pi1 = NULL;
    int *ptr;
    int *t_pi1   = NULL; /* Number of primes in prime decomposition of each pi */
    int *gi      = NULL; /* Prime roots of pi^ei                               */
    int *fi      = NULL; /* Copy of ei-1 because it's the indice in Kif        */
    int *pifi    = NULL; /* Copy of pi^ei                                      */
    int *rp      = NULL; /* */
    int *Li      = NULL; /* gcd(Ki, lcm(Kh .. Kt)) with h=0/1 (q even or odd)  */
    int *si      = NULL; /* */
    int *diLi    = NULL; /* di * Li                                            */
    int *Mg      = NULL; /* */
    int *vMg     = NULL; /* */
    int *Kif     = NULL; /* */
    int *Nif     = NULL; /* */
    int *dif     = NULL; /* */

    int i, j, s;
    int q, t = 0, ndiv, ht, div;
    int cl, nl, nlead;

    ptr = (int *)malloc( ((3*PWR_MAXSIZE + 8)*PRIME_MAXSIZE + 4 + 2*SIZE_MG) * sizeof(int) );
    t_pi1 = ptr;                                /* plasma_malloc(t_pi1, PRIME_MAXSIZE,             int); */
    gi    = t_pi1 + PRIME_MAXSIZE;              /* plasma_malloc(gi   , PRIME_MAXSIZE,             int); */
    fi    = gi    + PRIME_MAXSIZE;              /* plasma_malloc(fi   , PRIME_MAXSIZE,             int); */
    pifi  = fi    + PRIME_MAXSIZE;              /* plasma_malloc(pifi , PRIME_MAXSIZE,             int); */
    rp    = pifi  + PRIME_MAXSIZE;              /* plasma_malloc(rp   , PRIME_MAXSIZE+1,           int); */
    Li    = rp    + PRIME_MAXSIZE+1;            /* plasma_malloc(Li   , PRIME_MAXSIZE+1,           int); */
    si    = Li    + PRIME_MAXSIZE+1;            /* plasma_malloc(si   , PRIME_MAXSIZE+1,           int); */
    diLi  = si    + PRIME_MAXSIZE+1;            /* plasma_malloc(diLi , PRIME_MAXSIZE+1,           int); */
    Kif   = diLi  + PRIME_MAXSIZE+1;            /* plasma_malloc(Kif  , PRIME_MAXSIZE*PWR_MAXSIZE, int); */
    Nif   = Kif   + PRIME_MAXSIZE*PWR_MAXSIZE;  /* plasma_malloc(Nif  , PRIME_MAXSIZE*PWR_MAXSIZE, int); */
    dif   = Nif   + PRIME_MAXSIZE*PWR_MAXSIZE;  /* plasma_malloc(dif  , PRIME_MAXSIZE*PWR_MAXSIZE, int); */
    Mg    = dif   + PRIME_MAXSIZE*PWR_MAXSIZE;  /* plasma_malloc(Mg   , SIZE_MG,                   int); */
    vMg   = Mg    + SIZE_MG;                    /* plasma_malloc(vMg  , SIZE_MG,                   int); */
    
    pr_pi1 = (primedec_t**)malloc(PRIME_MAXSIZE*sizeof(primedec_t*));
    for(i=0; i<PRIME_MAXSIZE; i++) {
        pr_pi1[i] = (primedec_t*)malloc(PRIME_MAXSIZE*sizeof(primedec_t));
    }
    q = me*ne - 1;

    /* Fill-in pr_q, t, pr_pi1, t_pi1, gi, Nif, Kif and dif */
    GKK_prepare(q, ne, pr_q, &t, pr_pi1, t_pi1, gi, Nif, Kif, dif);
#ifdef DEBUG_IPT
    GKK_output_tables(me, ne, q, pr_q, t, gi, Nif, Kif, dif);
#endif

    ht = t;
    if( (q % 2) == 0 )
        ht = t + 1;

    ndiv = 1;
    for(i=0; i<t; i++) {
        fi[i]   = pr_q[i].e;
        pifi[i] = pr_q[i].pe;
        ndiv = ndiv * (pr_q[i].e + 1);
    }

    /*
     * First loop to compute number of leaders
     */
    /* loop over divisors v of q */
    nlead = 0;
    for (div=0; div<ndiv-1; div++) {
        GKK_L(t, pr_q, fi, Kif, dif, Li, diLi, &cl, &nl);

        nlead += nl;

        /* step to next divisor v of q (q/v = product of pifi) */
        for(i=0; i<t; i++) {
            if( fi[i] == 0 ) {
                fi[i]   = pr_q[i].e;
                pifi[i] = pr_q[i].pe;
            }
            else {
                fi[i]   = fi[i] - 1;
                pifi[i] = pifi[i] / pr_q[i].p;
                break;
            }
        }
    }

    *nleaders = nlead;
    /*fprintf(stderr, "Number of leader : %ld => ", (long)nlead); */

    /*
     * Second loop to store leaders
     */
    (*leaders) = (int*) malloc (nlead*3*sizeof(int));

    /* Restore fi and pifi */
    for(i=0; i<t; i++) {
      fi[i]   = pr_q[i].e;
      pifi[i] = pr_q[i].pe;
    }

    /* loop over divisors v of q */
    nlead = 0;
    for (div=0; div<ndiv-1; div++) {
        GKK_L(t, pr_q, fi, Kif, dif, Li, diLi, &cl, &nl);

        if( div == 0 ) {
            GKK_precompute_terms(q, pr_q, t, gi, diLi, rp, Mg, SIZE_MG);
            memcpy(vMg, Mg, SIZE_MG*sizeof(int));
        }
        else {
            for(i=0; i<t; i++) {
                if( pifi[i] != pr_q[i].pe ) {
                    for(j = rp[i]; j<rp[i]+diLi[i]; j++) {
                        vMg[j] = ((pr_q[i].pe / pifi[i])*Mg[j]) % q;
                    }
                }
                else {
                    memcpy(&(vMg[rp[i]]), &(Mg[rp[i]]), diLi[i]*sizeof(int));
                }
            }
        }

        for (i=0;i<ht; i++)
            si[i] = 0;
        while (1) {
            /* convert current leader from additive to multiplicative domain */
            s = 0;
            for (i=0; i<t; i++) {
                if( diLi[i] == 0 )
                    continue;
                s = (s + vMg[rp[i] + si[i]]) % q;
            }

            /* assign it to owner */
            (*leaders)[nlead  ] = s;
            (*leaders)[nlead+1] = cl;
            //leaders[nleaders+2] = owner;
            nlead += 3;

            nl = nl - 1;
            if( nl == 0 )
                break;

            /* step to next leader */
            for(i=0; i<ht; i++) {
                if( diLi[i] == 0 ) continue;
                si[i] = si[i] + 1;
                if( si[i] < diLi[i] ) {
                    if( (i == (ht-1)) && (ht != t) ) {
                        /* flip vMg for i=1 */
                        for(j=0; j<diLi[0]; j++) {
                            vMg[rp[0]+j] = (q-vMg[rp[0]+j]) % q;
                        }
                    }
                    break;
                }
                else
                    si[i] = 0;
            }
        }

        /* step to next divisor v of q (q/v = product of pifi) */
        for(i=0; i<t; i++) {
            if( fi[i] == 0 ) {
                fi[i]   = pr_q[i].e;
                pifi[i] = pr_q[i].pe;
            }
            else {
                fi[i]   = fi[i] - 1;
                pifi[i] = pifi[i] / pr_q[i].p;
                break;
            }
        }
    }
    
#ifdef DEBUG_IPT
    printf("nleaders : %d\n", *nleaders);
    printf("leaders  : ");
    for(i=0; i<*nleaders; i++)
      {
        printf(" %d", (*leaders)[i*3]);
        printf(" %d", (*leaders)[i*3+1]);
        printf(" %d", (*leaders)[i*3+2]);
      }
    printf("\n");
#endif

    for(i=0; i<PRIME_MAXSIZE; i++)
        free(pr_pi1[i]);
    free(pr_pi1);
    free(ptr);

    return PLASMA_SUCCESS;
}

Here is the call graph for this function:

Here is the caller graph for this function:

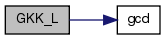
void GKK_L	(	int	t,
		primedec_t *	pr_q,
		int *	fi,
		int *	Kif,
		int *	dif,
		int *	Li,
		int *	diLi,
		int *	cl,
		int *	nl
	)

---

GKK_L computes Li, cycle length cl, and number of leaders nl.

See also:

GKK_prepare

Parameters:

[in]	t	Number of primes in prime decomposition of q
[in]	pr_q	Prime Decomposition of q
[in]	fi	Array of dimension PWR_MAXSIZE
[in]	Kif	Array of dimension PWR_MAXSIZE*PRIME_MAXSIZE Stores the multiplicative order of n modulo pi^ei
[in]	dif	Array of dimension PWR_MAXSIZE*PRIME_MAXSIZE dif(i,j) = Nif(i,j) / Kif(i,j)
[out]	Li	Array of dimension PWR_MAXSIZE
[out]	diLi	Array of dimension PWR_MAXSIZE diLi(i) = di(i) * Li (i) (bound for the leaders sets)
[out]	cl	Cycle length
[out]	nl	Number of leaders

Definition at line 462 of file gkkleader.c.

References gcd(), and PWR_MAXSIZE.

                                                 {
    int i, lcl, lnl;

    /* compute cycle length (cl) and Li */
    lcl = 1;
    for (i=0; i<t; i++) {
        if( fi[i] == 0 ) {
            Li[i] = 1;
        }
        else {
            Li[i] = gcd( Kif[i*PWR_MAXSIZE+fi[i]-1], lcl);
            lcl = (lcl * Kif[i*PWR_MAXSIZE+fi[i]-1]) / Li[i];
        }
    }

    if( pr_q[0].p == 2 ) {
        if( fi[0] == 0 ) {
            Li[t] = 1;
        }
        else {
            int tmp = Kif[t*PWR_MAXSIZE+fi[0]-1];

            Li[t] = gcd( tmp, lcl);
            lcl = (lcl * tmp) / Li[t];
        }
    }
    *cl = lcl;

    /* count number of cycles (nl) and compute di*Li */
    lnl = 1;
    for (i=0; i<t; i++) {
        if( fi[i] != 0 ) {
            diLi[i] = dif[i*PWR_MAXSIZE+fi[i]-1] * Li[i];
            lnl = lnl * diLi[i];
        }
        else 
            diLi[i] = 0;
    }
    if( pr_q[0].p == 2 ) {
        if( fi[0] != 0 ) {
            diLi[t] = dif[t*PWR_MAXSIZE+fi[0]-1] * Li[t];
            lnl = lnl * diLi[t];
        }
        else
            diLi[t] = 0;
    }
    *nl = lnl;

#ifdef DEBUG_IPT
    printf("nl : %d\n", lnl);
    printf("cl : %d\n", lcl);
    printf("Li   :");
    for(i=0; i<t+1; i++)
      printf(" %d", Li[i]);
    printf("\n");
    printf("diLi :");
    for(i=0; i<t+1; i++)
      printf(" %d", diLi[i]);
    printf("\n");
#endif
}

Here is the call graph for this function:

Here is the caller graph for this function:

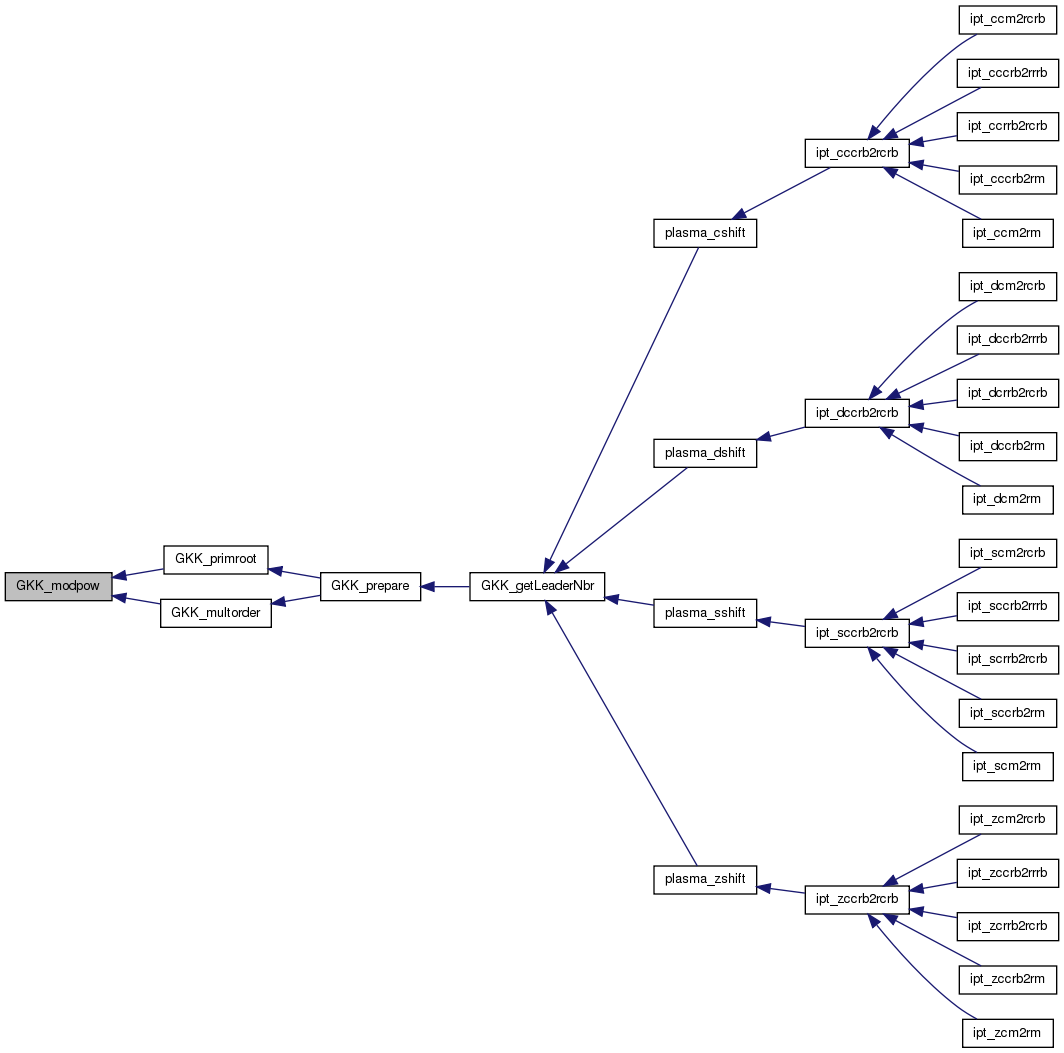
int GKK_modpow	(	int *	dt,
		int	e,
		int	m
	)

---

GKK_modpow computes x^e mod m, like the modpow function. Unlike modpow, x is given implicitly via its doubling table dt.

See also:

GKK_doublingtable

Parameters:

[in]	dt	Array of x^i mod m.
[in]	e
[in]	m

Returns:

Return values:

x^e

mod m

Definition at line 102 of file gkkleader.c.

                                      {
    int64_t y8, m8;
    int     z, i;

    m8 = m;
    y8 = 1;
    z  = e;
    i  = 0;

    /* dt size is not tested because tested before in GKK_doublingtable */
    while( z > 0 ) {
        if( (z%2) == 1 ) 
            y8 = (y8*dt[i]) % m8;
        z = z / 2;
        i++;
    }
    return (int)y8;
}

Here is the caller graph for this function:

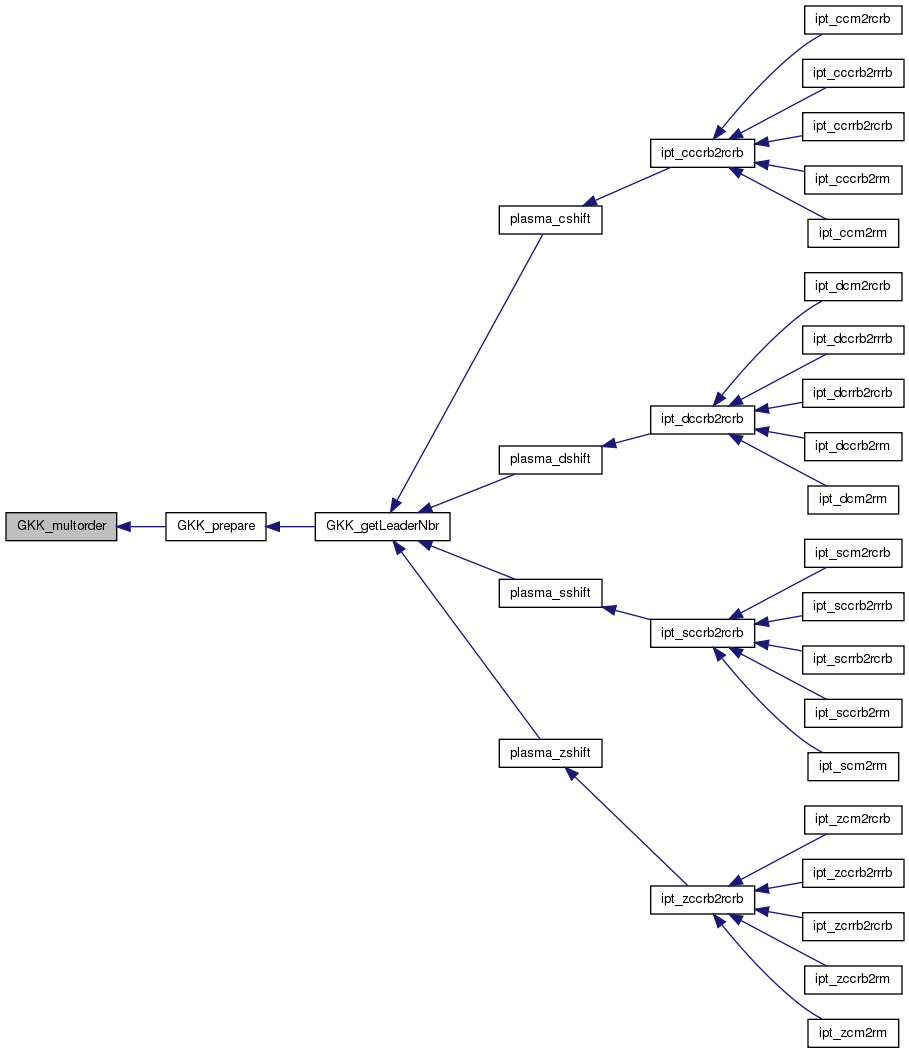
int GKK_multorder	(	int	n,
		int	p,
		int	e,
		int	pe,
		primedec_t *	pr_p1,
		int	t_p1
	)

---

GKK_multorder finds the multiplicative order of n modulo p^e = pe, given the prime decomposition of p-1.

See also:

GKK_doublingtable

GKK_modpow

Parameters:

[in]	n
[in]	p
[in]	e
[in]	pe
[in,out]	pr_p1	On entry, prime decomposition of p - 1 On exit, prime decomposition of p - 1 and p^(e-1) appends at the end
[in]	t_p1	Number of primes in prime decomposition of p-1

Returns:

Return values:

the	multiplicative order of n modulo p^e = pe

Definition at line 232 of file gkkleader.c.

References primedec::e, GKK_doublingtable(), GKK_modpow(), primedec::p, primedec::pe, PRIME_MAXSIZE, and PWR_MAXSIZE.

                                                                            {
    int fi[PRIME_MAXSIZE], dt[PWR_MAXSIZE];
    int t, i, K1, c;
    int K;

    /* append p^(e-1) to the prime decomposition of p-1 */
    t = t_p1;
    if( e > 1 ) {
        pr_p1[t].p  = p;
        pr_p1[t].e  = e-1;
        pr_p1[t].pe = pe / t;
        t = t_p1 + 1;
    }

    GKK_doublingtable(n, pe, pe-1, dt);

    for (i=0; i<PRIME_MAXSIZE; i++) 
        fi[i] = pr_p1[i].e;

    K = pe - pe/p;
    for(i=0; i<t; i++) {
        while( fi[i] > 0 ) {
            K1 = K / pr_p1[i].p;
            c = GKK_modpow(dt, K1, pe);
            if( c == 1 ) {
                K = K1;
                fi[i] = fi[i] - 1;
            }
            else {
                break;
            }
        }
    }
    return K;
}

Here is the call graph for this function:

Here is the caller graph for this function:

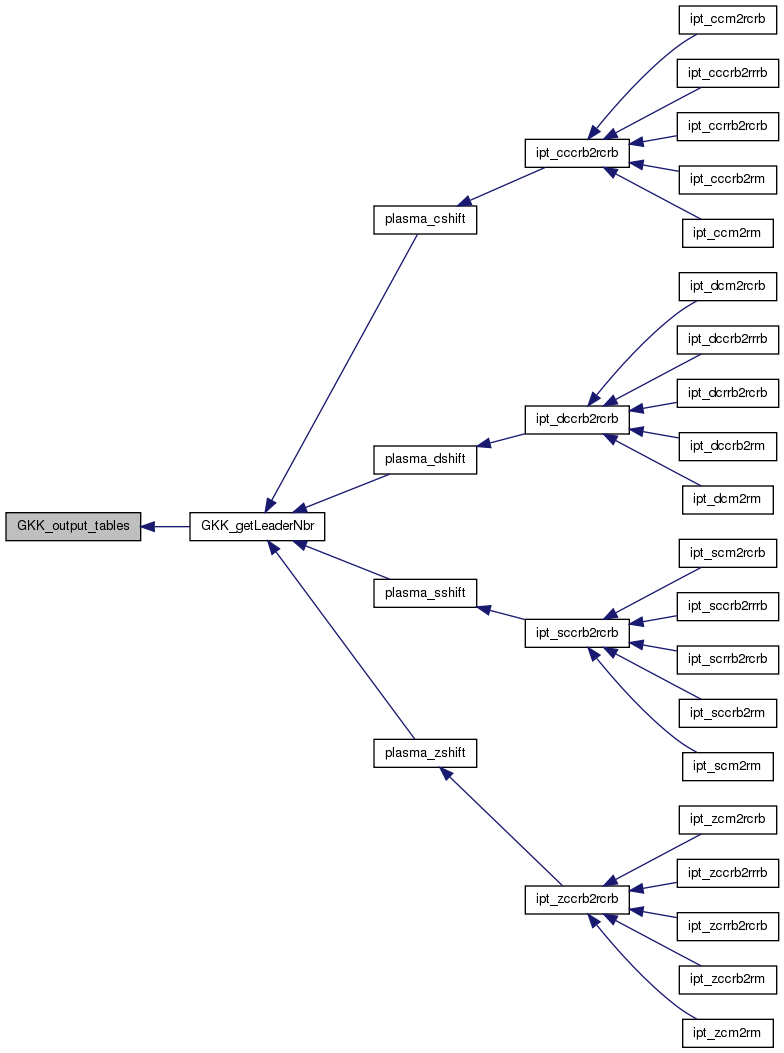
void GKK_output_tables	(	int	m,
		int	n,
		int	q,
		primedec_t *	pr_q,
		int	t,
		int *	gi,
		int *	Nif,
		int *	Kif,
		int *	dif
	)

---

GKK_output_tables prints information from the heart of the GKK algorithm in a human friendly format.

Parameters:

[in]	m
[in]	n
[in]	q
[in]	pr_q	Prime Decomposition of q
[in]	t	Number of primes in prime decomposition of q
[in]	gi	Array of size PRIME_MAXSIZE Stores prime root of each pi^ei
[in]	Nif	Array of dimension PWR_MAXSIZE*PRIME_MAXSIZE Stores the Phi(pi^fi) with fi in (1 .. ei)
[in]	Kif	Array of dimension PWR_MAXSIZE*PRIME_MAXSIZE Stores the multiplicative order of n modulo pi^ei
[in]	dif	Array of dimension PWR_MAXSIZE*PRIME_MAXSIZE dif(i,j) = Nif(i,j) / Kif(i,j)

Definition at line 707 of file gkkleader.c.

References primedec::e, lapack_testing::f, and PWR_MAXSIZE.

                                                              {
    int i, f;

    fprintf(stdout, "Information from the GKK algorithm\n");
    fprintf(stdout, "==================================\n");
    fprintf(stdout, "m = %4d\n", m);
    fprintf(stdout, "n = %4d\n", n);
    fprintf(stdout, "q = %4d\n", q);
    for (i=0; i<t; i++) {
        fprintf(stdout, "==================================\n");
        fprintf(stdout, "       i = %4d\n", i+1      );
        fprintf(stdout, "       p = %4d\n", pr_q[i].p);
        fprintf(stdout, "       e = %4d\n", pr_q[i].e);
        fprintf(stdout, "     p^e = %4d\n", pr_q[i].pe);
        if( pr_q[i].p != 2 )
            fprintf(stdout, "       g = %4d\n", gi[i]);
        else
            fprintf(stdout, "mod(n,4) = %4d\n", n%4);
        
        fprintf(stdout, "\n");
        fprintf(stdout, "    f | ");
        for (f=0; f<pr_q[i].e; f++)
            fprintf(stdout, "%4d ", f+1);
        fprintf(stdout, "\n");
        fprintf(stdout, "----------------------------------\n");

        fprintf(stdout, "Ni(f) | ");
        for (f=0; f<pr_q[i].e; f++)
            fprintf(stdout, "%4d ", Nif[i*PWR_MAXSIZE+f]);
        fprintf(stdout, "\n");

        fprintf(stdout, "Ki(f) | ");
        for (f=0; f<pr_q[i].e; f++)
            fprintf(stdout, "%4d ", Kif[i*PWR_MAXSIZE+f]);
        fprintf(stdout, "\n");

        fprintf(stdout, "di(f) | ");
        for (f=0; f<pr_q[i].e; f++)
            fprintf(stdout, "%4d ", dif[i*PWR_MAXSIZE+f]);
        fprintf(stdout, "\n");
        fprintf(stdout, "\n");
    }
}

Here is the caller graph for this function:

void GKK_precompute_terms	(	int	q,
		primedec_t *	pr_q,
		int	t,
		int *	gi,
		int *	diLi,
		int *	rp,
		int *	Mg,
		int	nMg
	)

---

GKK_precompute_terms Precompute M*g^i mod q.

See also:

GKK_prepare

Parameters:

[in]	q
[in]	pr_q	Prime Decomposition of q
[in]	t	Number of primes in prime decomposition of q
[in]	gi	Array of dimension PWR_MAXSIZE
[in]	diLi	Array of dimension PWR_MAXSIZE
[out]	rp	Array of dimension PWR_MAXSIZE rp(i) = sum(diLi(i), i=0..i-1), rp(0) = 0;
[out]	Mg	Array of dimension nMg
[in]	nMg

Definition at line 563 of file gkkleader.c.

References primedec::pe, and plasma_error().

                                                                {
    int i, j, nMg_needed, ht;

    ht = t;
    if( pr_q[0].p == 2 ) 
        ht = t + 1;

    nMg_needed = diLi[0];
    for(i=1; i<ht; i++)
        nMg_needed += diLi[i];

    if( nMg_needed > nMg ) {
        plasma_error(__func__, "the size of Mg is not large enough");
        return;
    }

    rp[0] = 0;
    for(i=0; i<t; i++) {
        if( pr_q[i].p != 2 ) {
            Mg[rp[i]] = q / pr_q[i].pe;

            for(j=1; j<diLi[i]; j++) 
                Mg[rp[i]+j] = (Mg[rp[i]+j-1]*gi[i]) % q;
        }
        rp[i+1] = rp[i] + diLi[i];
    }
    if( pr_q[0].p == 2 ) {
        Mg[rp[0]] = q / pr_q[0].pe;
        for(j=1; j<diLi[0]; j++) 
            Mg[rp[0]+j] = (Mg[rp[0]+j-1]*5) % q;
    }

#ifdef DEBUG_IPT
    printf("t  : %d\n", t);
    printf("ht : %d\n", ht);
    printf("rp :");
    for(i=0; i<ht; i++)
      printf(" %d", rp[i]);
    printf("\n");
    printf("Mg :");
    for(i=0; i<nMg; i++)
      printf(" %d", Mg[i]);
    printf("\n");
#endif
}

Here is the call graph for this function:

Here is the caller graph for this function:

void GKK_prepare	(	int	q,
		int	n,
		primedec_t *	pr_q,
		int *	t,
		primedec_t **	pr_pi1,
		int *	t_pi1,
		int *	gi,
		int *	Nif,
		int *	Kif,
		int *	dif
	)

---

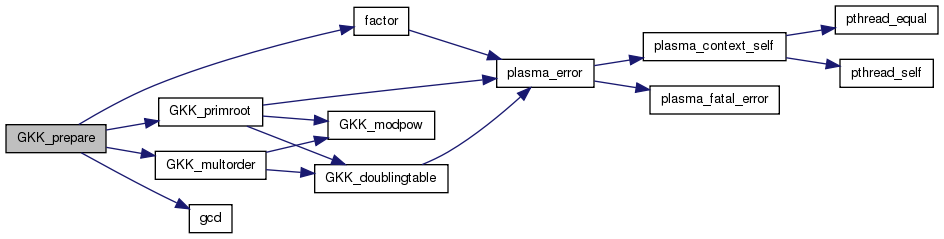
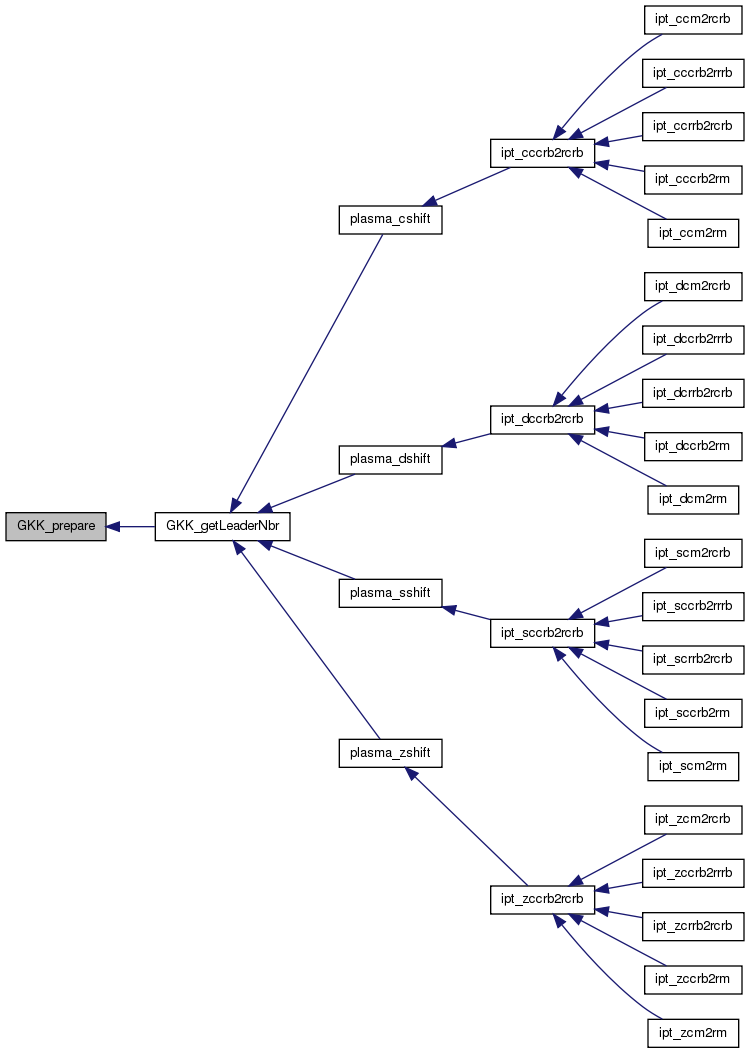
GKK_prepare Prepare for the generation of leaders.

See also:

GKK_primroot

GKK_multorder

factor

gcd

Parameters:

[in]	q	= mn - 1
[in]	n
[out]	pr_q	Prime Decomposition of q
[out]	t	Number of primes in prime decomposition of q
[out]	pr_pi1	Array of prime decompositions of each pi in prime decomposition of q
[out]	t_pi1	Array of number of primes in each prime decomposition of pi found in prime decomposition of q
[out]	gi	Array of size PRIME_MAXSIZE Stores prime root of each pi^ei
[out]	Nif	Array of dimension PWR_MAXSIZE*PRIME_MAXSIZE Stores the Phi(pi^fi) with fi in (1 .. ei) Phi(k) is the number of positive integers less than or equal to k which are coprime to k.
[out]	Kif	Array of dimension PWR_MAXSIZE*PRIME_MAXSIZE Stores the multiplicative order of n modulo pi^ei
[out]	dif	Array of dimension PWR_MAXSIZE*PRIME_MAXSIZE dif(i,j) = Nif(i,j) / Kif(i,j)

Definition at line 318 of file gkkleader.c.

References primedec::e, lapack_testing::f, factor(), gcd(), GKK_multorder(), GKK_primroot(), primedec::p, and PWR_MAXSIZE.

                                               { 
    int i, f, p1f, tmp;
           
    /* factor q */
    factor(q, pr_q, t);

    /* factor pi-1 for each pi in q */
    for (i=0; i<*t; i++) 
        factor(pr_q[i].p-1, pr_pi1[i], &(t_pi1[i]));
    
    /* 
     * Compute the number of positive integers coprime 
     * to f, Ni(f) for f = 1, 2, ..., ei 
     */
    for (i=0; i<*t; i++) {
        tmp = PWR_MAXSIZE*i;
        Nif[tmp] = pr_q[i].p - 1;

        for(f=1; f < pr_q[i].e; f++) 
            Nif[tmp+f] = pr_q[i].p * Nif[tmp+f-1];
    }
    
    if( pr_q[0].p == 2 ) {
        for(f=1; f < pr_q[0].e; f++) 
            Nif[f] = Nif[f] / 2;

        Nif[PWR_MAXSIZE*(*t)] = 1;
        for(f=1; f < pr_q[0].e; f++) 
          Nif[PWR_MAXSIZE*(*t)+f] = 2;
    }
    
    /*
     * Case A: odd pi
     */
    for(i=0; i <*t; i++) {
        if( pr_q[i].p != 2 ) {
            tmp = PWR_MAXSIZE*i;

            /* compute Ki(ei) */
            Kif[tmp+pr_q[i].e-1] = GKK_multorder(n, pr_q[i].p, pr_q[i].e, pr_q[i].pe, pr_pi1[i], t_pi1[i]);

            /* compute Ki(f) for f = 1, 2, ..., ei-1 */
            for(f = pr_q[i].e-2;  f>-1; f--) {
                if( Kif[tmp+f+1] >= pr_q[i].p )
                    Kif[tmp+f] = Kif[tmp+f+1] / pr_q[i].p;
                else
                    Kif[tmp+f] = Kif[tmp+f+1];
            }

            /* compute di(f) for f = 1, 2, ..., ei */
            for(f=0; f<pr_q[i].e; f++)
                dif[tmp+f] = Nif[tmp+f] / Kif[tmp+f];

            /* compute primitive root gi for pi^ei */
            if( dif[tmp+pr_q[i].e-1] == 1 ) 
                /* special case where n is already a primitive root*/
                gi[i] = n % pr_q[i].pe;
            else
                /* general case requiring a search for a primitive root */
                gi[i] = GKK_primroot(pr_q[i].p, pr_q[i].e, pr_pi1[i], t_pi1[i]);
        }
    }

   /*
    * Case B: even pi (only the first one)
    */
    if( pr_q[0].p == 2 ) {
        /* reset primitive root */
        gi[0] = 0;

        /* compute d1(f) for f = 1,2,...,e1 */
        p1f = 2;
        for (f=0; f<pr_q[0].e; f++) {
            if( (n%4) == 1)
                dif[f] = gcd( (    (n%p1f)-1)/4, Nif[f] );
            else
                dif[f] = gcd( (p1f-(n%p1f)-1)/4, Nif[f] );
            p1f = p1f*2;
        }

        /* compute K1(f) for f = 1,2,...,e1 */
        for (f=0; f<pr_q[0].e; f++)
            Kif[f] = Nif[f] / dif[f];

        /* compute K0(f) for f = 1,2,...,e1 */
        tmp = PWR_MAXSIZE * (*t);
        Kif[tmp] = 1;
        for (f=1; f<pr_q[0].e; f++) {
            Kif[tmp+f] = 2;
            if( (n%4) == 1 ) 
                Kif[tmp+f] = 1;
        }

        /* compute d0(f) for f = 1,2,...,e1 */
        for (f=0; f<pr_q[0].e; f++)
            dif[tmp+f] = Nif[tmp+f] / Kif[tmp+f];
    }
}

Here is the call graph for this function:

Here is the caller graph for this function:

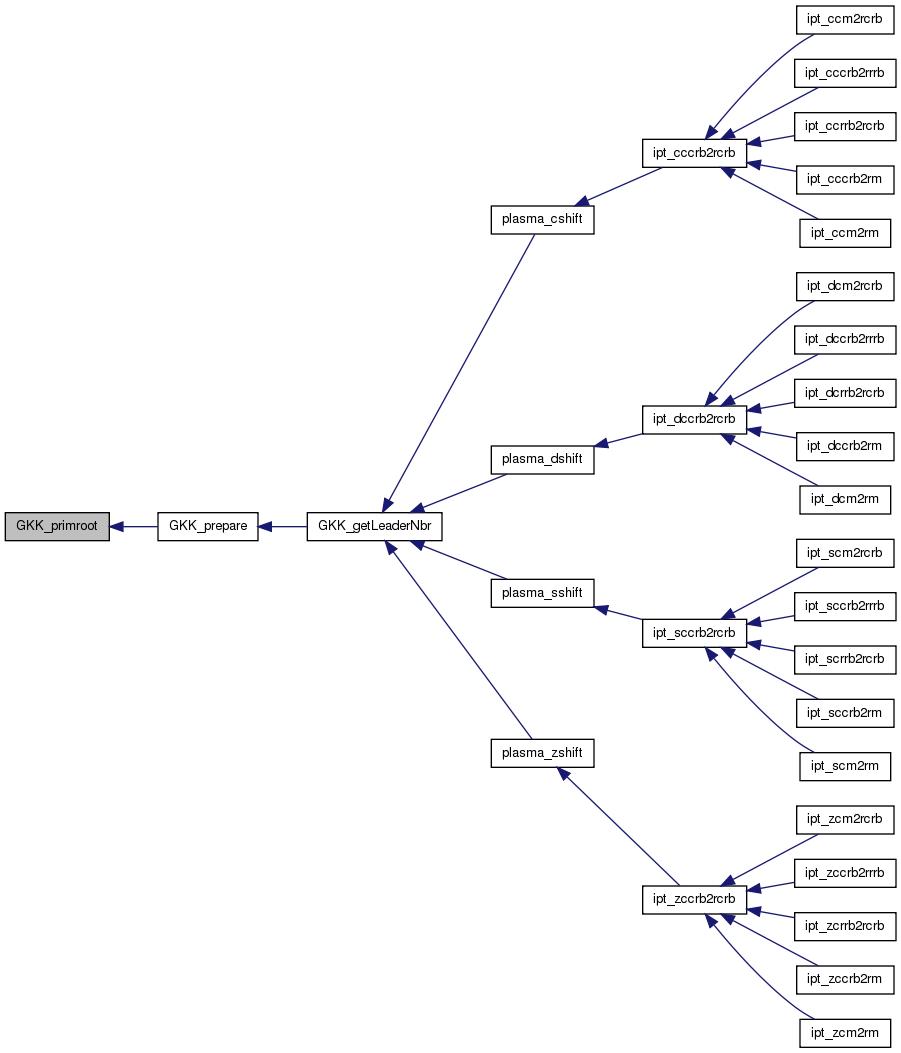
int GKK_primroot	(	int	p,
		int	e,
		primedec_t *	pr_p1,
		int	t_p1
	)

Definition at line 150 of file gkkleader.c.

References GCAND_SIZE, GKK_doublingtable(), GKK_modpow(), plasma_error(), and PWR_MAXSIZE.

                                                            {
    static int gcand[GCAND_SIZE] = { 
        2,   3,  5,  6,  7, 10, 11, 12, 13, 14,
        15, 17, 18, 19, 20, 21, 22, 23, 24, 26,
        28, 29, 30, 31, 33, 34, 35, 37, 38, 39,
        41, 43, 44, 46, 47, 51, 52, 53, 55, 57,
        58, 59, 60, 62, 69, 73 };

    int dt[PWR_MAXSIZE];
    int i, j, p2, c, g;
    int ok;

    p2 = p;
    if( e >= 2 ) 
        p2 = p*p;

    /* try candidates */
    for(i=0; i < GCAND_SIZE; i++) {
        g = gcand[i];
        GKK_doublingtable(g, p2, p-1, dt);
        
        ok = 1;

        for(j=0; j<t_p1; j++) {
            c = GKK_modpow(dt, (p-1) / pr_p1[j].p, p2);
            if( (c % p) == 1 ) {
                ok = 0;
                break;
            }
        }
        if( ok == 1 ) 
            break;
    }

    if( ok != 1 ) {
        plasma_error(__func__, "failed to find a primitive root");
        return -1;
    }
    /* check that g is a primitive root also for p^k for all k */
    if( e >= 2 ) {
        c = GKK_modpow(dt, p-1, p2);
        if( c == 1 ) {
            /* g is not a primitive root for p^k, but g+p is */
             g = g + p;
        }
    }
    return g;
}

Here is the call graph for this function:

Here is the caller graph for this function: