PLASMA  2.4.5
PLASMA - Parallel Linear Algebra for Scalable Multi-core Architectures
 All Data Structures Namespaces Files Functions Variables Typedefs Enumerations Enumerator Macros Groups
Data Structures | Macros | Typedefs | Functions
primes.h File Reference
This graph shows which files directly or indirectly include this file:

Go to the source code of this file.

Data Structures

struct  primedec

Macros

#define IMBALANCE_THRESHOLD   10
#define PWR_MAXSIZE   32
#define PRIME_MAXSIZE   10
#define SIZE_MG   1024
#define SIZE_LEADERS   1023
#define min(a, b)   ((a<b)?a:b)
#define max(a, b)   ((a>b)?a:b)

Typedefs

typedef struct primedec primedec_t

Functions

int lcm (int a, int b)
int gcd (int a, int b)
int modpow (int x, int n, int m)
void factor (int n, primedec_t *pr, int *nf)
int minloc (int n, int *T)
int64_t maxval (int n, int *T)
int64_t sum (int n, int *T)

Detailed Description

PLASMA InPlaceTransformation module PLASMA is a software package provided by Univ. of Tennessee, Univ. of California Berkeley and Univ. of Colorado Denver

This work is the implementation of an inplace transformation based on the GKK algorithm by Gustavson, Karlsson, Kagstrom and its fortran implementation.

Version:
2.4.5
Author:
Mathieu Faverge
Date:
2010-11-15

Definition in file primes.h.

Macro Definition Documentation

#define IMBALANCE_THRESHOLD   10

Definition at line 22 of file primes.h.

#define max (   a,
  b 
)    ((a>b)?a:b)

Definition at line 33 of file primes.h.

#define min (   a,
  b 
)    ((a<b)?a:b)

Definition at line 29 of file primes.h.

#define PRIME_MAXSIZE   10

Definition at line 24 of file primes.h.

#define PWR_MAXSIZE   32

Definition at line 23 of file primes.h.

#define SIZE_LEADERS   1023

Definition at line 26 of file primes.h.

#define SIZE_MG   1024

Definition at line 25 of file primes.h.

Typedef Documentation

typedef struct primedec primedec_t

Definition at line 43 of file primes.h.

Function Documentation

void factor ( int  n,
primedec_t *  pr,
int *  nf 
)

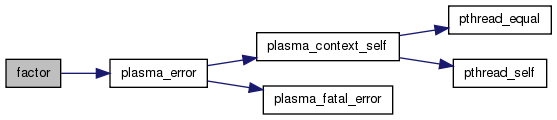
factor Factors an integer into a product of prime powers.

Parameters:
[in]n
[out]prArray of size PRIME_MAXSIZE On exit, contains the prime factor of n modulo m
[out]nfNumber of prime factor in n.

Definition at line 748 of file primes.c.

References primedec::e, lapack_testing::f, primedec::p, primedec::pe, plasma_error(), PRIME_MAXSIZE, primes, and PRIMESTABLE_SIZE.

{
int x, i, f, sqrtx, lnf;
lnf = 0;
x = n;
sqrtx = (int)sqrt((double)x);
i = 0;
f = 1;
while( x > 1 ) {
/* Get a prime f */
f = primes[i];
/* check if x is prime */
if( f > sqrtx ) {
if( lnf > PRIME_MAXSIZE ) {
plasma_error(__func__, "input matrix pr has too few columns");
}
pr[lnf].p = x;
pr[lnf].e = 1;
pr[lnf].pe = x;
lnf++;
break;
}
/* check if f | x */
if( (x % f) == 0 ) {
/* found a new prime factor of x, namely f */
if( lnf > PRIME_MAXSIZE ) {
plasma_error(__func__, "input matrix pr has too few columns");
}
pr[lnf].p = f;
pr[lnf].e = 1;
pr[lnf].pe = f;
x = x / f;
while( (x % f) == 0 ) {
x = x / f;
pr[lnf].e += 1;
pr[lnf].pe *= f;
}
sqrtx = (int)sqrt((double)x);
lnf++;
}
i++;
if( !(i < PRIMESTABLE_SIZE) ) {
plasma_error(__func__, "ran out of table");
}
}
*nf = lnf;
}

Here is the call graph for this function:

Here is the caller graph for this function:

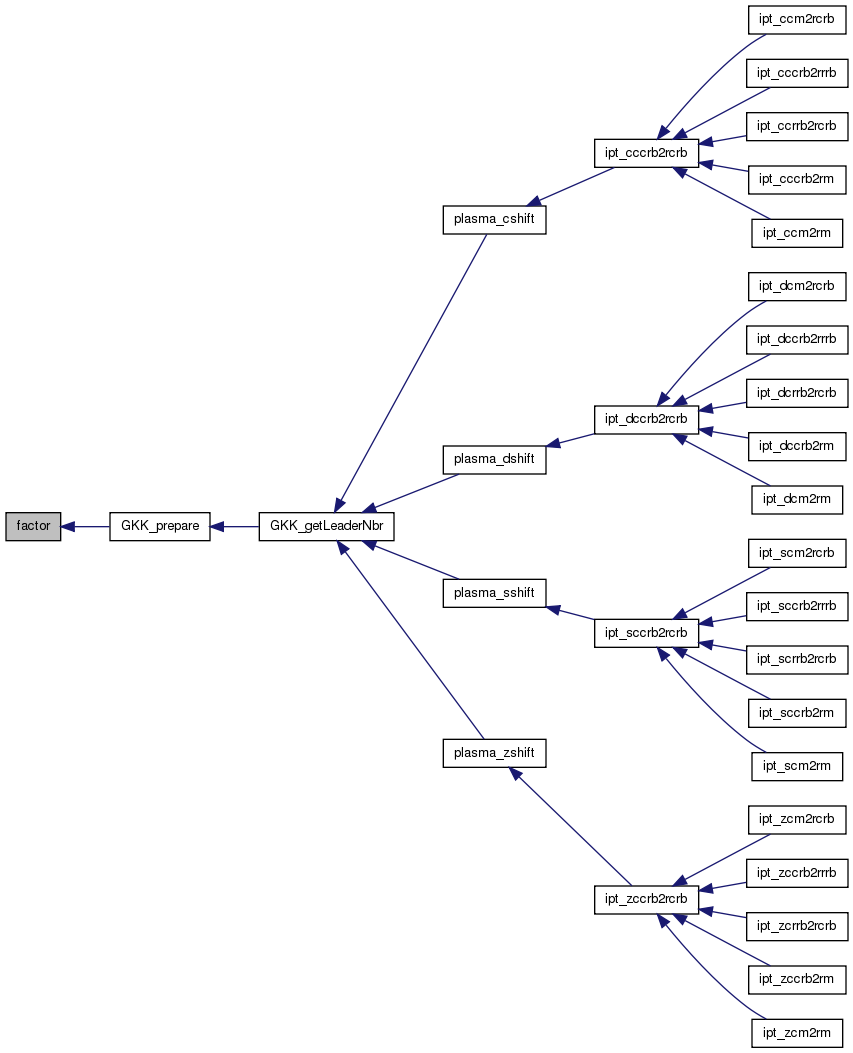
int gcd ( int  a,
int  b 
)

gcd computes the greatest common divisor of a and b.

Parameters:
[in]a
[in]b
Returns:
Return values:
thegreatest common divisor of a and b.

Definition at line 673 of file primes.c.

{
int x, y, t;
x = a;
y = b;
while( y != 0 ) {
t = y;
y = x%y;
x = t;
}
return x;
}

Here is the caller graph for this function:

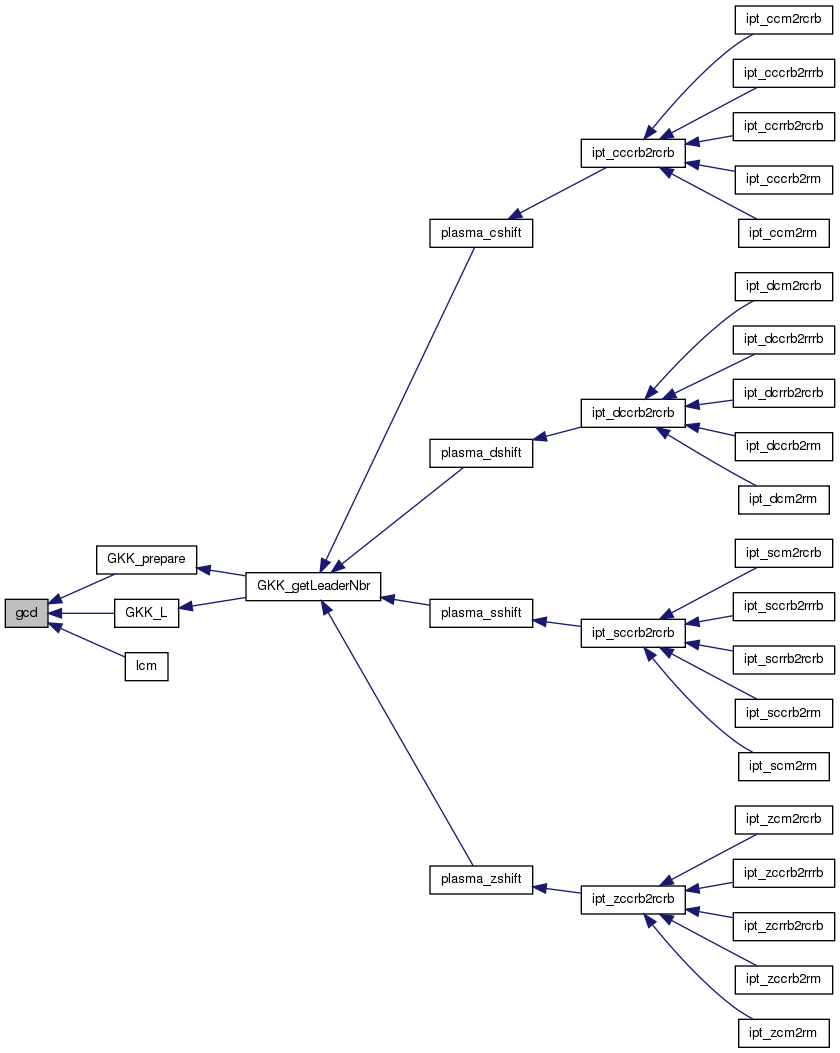
int lcm ( int  a,
int  b 
)

lcm computes the least common mutliple of a and b

Parameters:
[in]a
[in]b
Returns:
Return values:
theleast common multiple of a and b

Definition at line 651 of file primes.c.

References gcd().

{
return (a / gcd(a, b)) * b;
}

Here is the call graph for this function:

int64_t maxval ( int  n,
int *  T 
)

maxval return the maximum value found in T

Parameters:
[in]nSize of the array T
[in]TArray of integers of size n
Returns:
Return values:
themaximum found in T

Definition at line 857 of file primes.c.

References max.

{
int64_t max = T[0];
int i;
for (i=1; i<n; i++) {
if (T[i] > max)
max = T[i];
}
return max;
}

Here is the caller graph for this function:

int minloc ( int  n,
int *  T 
)

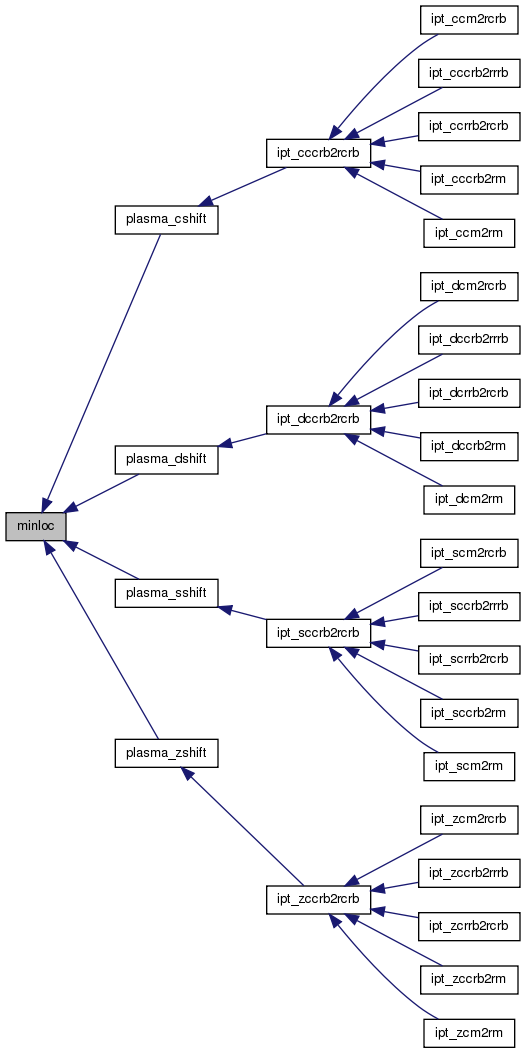
minloc return the indice of the minimum in array T

Parameters:
[in]nSize of the array T
[in]TArray of integers of size n
Returns:
Return values:
theindice of the minimum in T

Definition at line 823 of file primes.c.

{
int mini = 0;
int minT = T[0];
int i;
for (i=1; i<n; i++) {
if (T[i] < minT) {
minT = T[i];
mini = i;
}
}
return mini;
}

Here is the caller graph for this function:

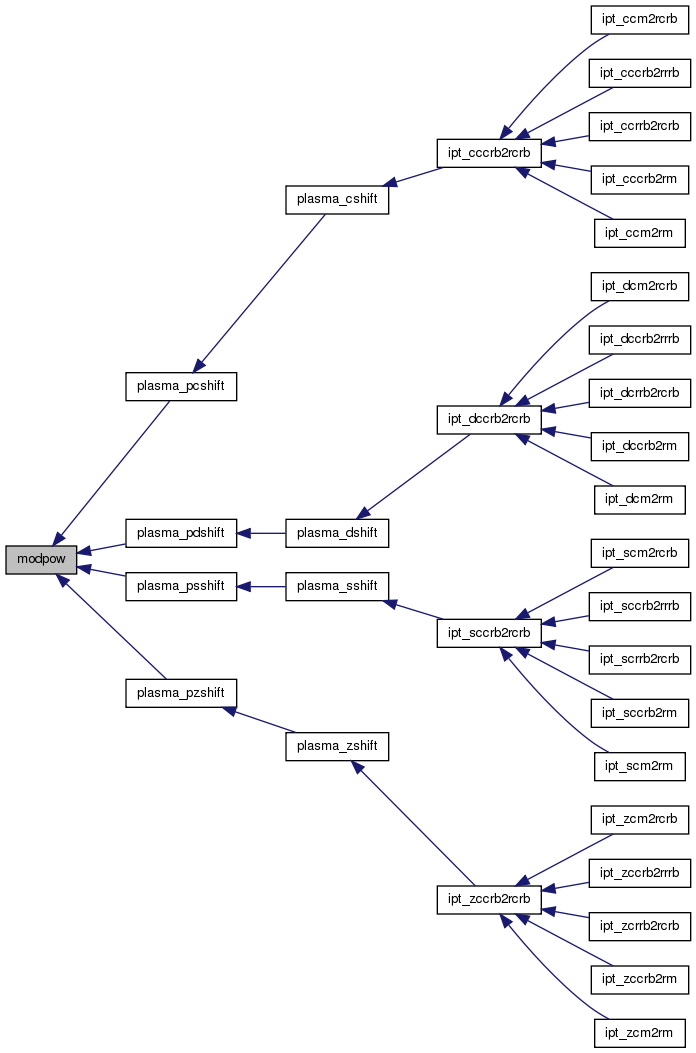
int modpow ( int  x,
int  n,
int  m 
)

modpow computes the modular power x^n mod m using recursive squaring. The number of operations is proportional to the logarithm of the exponent n.

Parameters:
[in]x
[in]n
[in]m
Returns:
Return values:
themodular power x^n mod m

Definition at line 707 of file primes.c.

{
int64_t Nn, y, z, t;
if( n == 0 )
return 1;
Nn = n;
y = 1;
z = x;
while (1) {
t = Nn % 2;
Nn = Nn / 2;
if( t != 0 ) {
y = (z*y) % m;
if( Nn == 0 )
return y;
}
z = (z * z) % m;
}
}

Here is the caller graph for this function:

int64_t sum ( int  n,
int *  T 
)

sum return the sum(T[i], i=0..n-1)

Parameters:
[in]nSize of the array T
[in]TArray of integers of size n
Returns:
Return values:
sum(T[i],i=0..n-1)

Definition at line 888 of file primes.c.

References sum().

{
int64_t sum = T[0];
int i;
for (i=1; i<n; i++)
sum += T[i];
return sum;
}

Here is the call graph for this function:

Here is the caller graph for this function: