primes.c File Reference

#include <stdlib.h>
#include <stdio.h>
#include <math.h>
#include "common.h"
#include "primes.h"

Include dependency graph for primes.c:

Go to the source code of this file.

Macros
#define	PRIMESTABLE_SIZE   4792

Functions
int	lcm (int a, int b)
int	gcd (int a, int b)
int	modpow (int x, int n, int m)
void	factor (int n, primedec_t *pr, int *nf)
int	minloc (int n, int *T)
int64_t	maxval (int n, int *T)
int64_t	sum (int n, int *T)

Variables
int	primes [PRIMESTABLE_SIZE]

---

Detailed Description

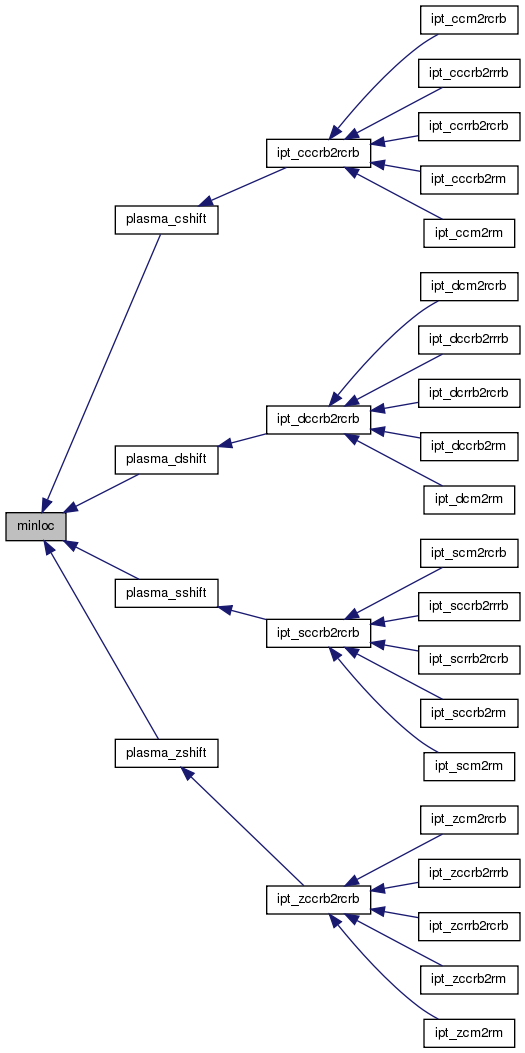
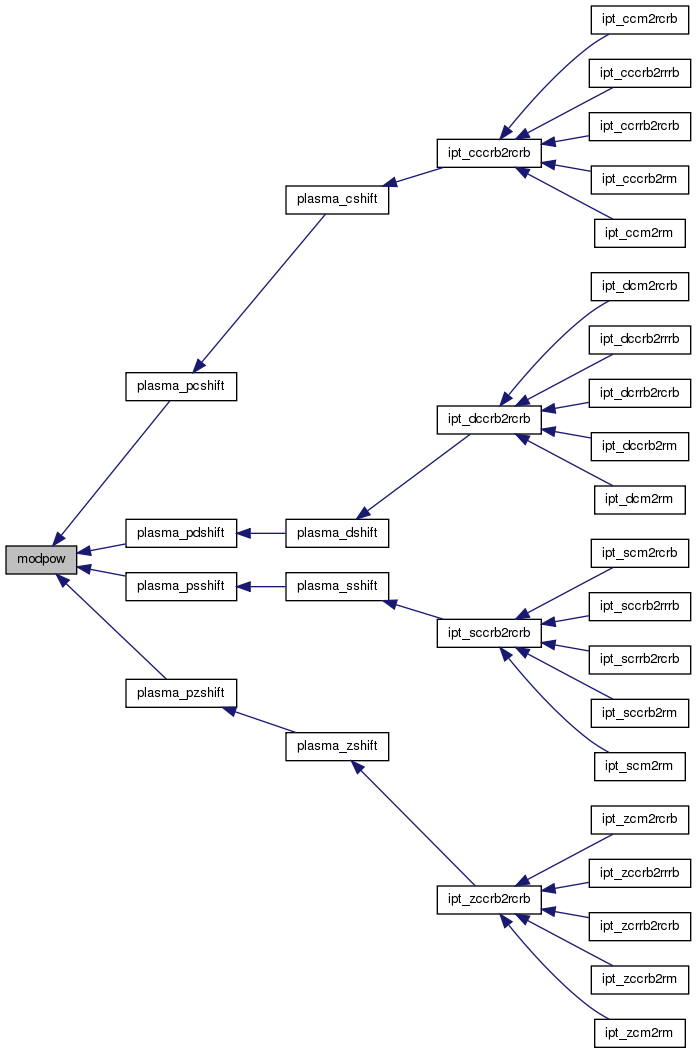
PLASMA InPlaceTransformation module PLASMA is a software package provided by Univ. of Tennessee, Univ. of California Berkeley and Univ. of Colorado Denver

This work is the implementation of an inplace transformation based on the GKK algorithm by Gustavson, Karlsson, Kagstrom and its fortran implementation.

Version:

2.4.5

Author:

Mathieu Faverge

Date:

2010-11-15

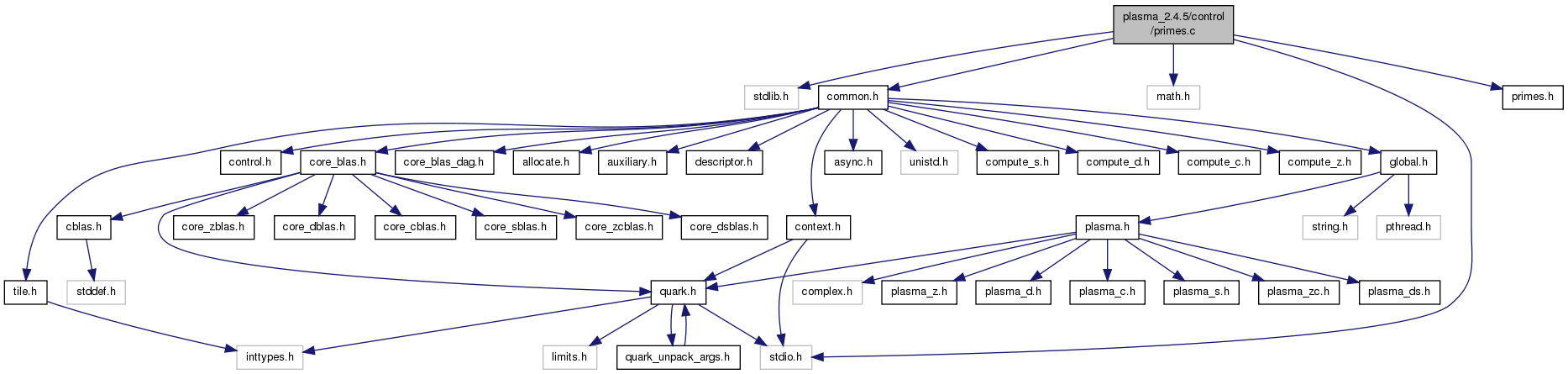
Definition in file primes.c.

---

Macro Definition Documentation

#define PRIMESTABLE_SIZE   4792

Table of all primes less than sqrt(2**31-1) (46341) in ascending order. (This table is not initialized in one go due to an internal compiler error in the PathScale F95 compiler that we use.)

Definition at line 29 of file primes.c.

---

Function Documentation

void factor	(	int	n,
		primedec_t *	pr,
		int *	nf
	)

---

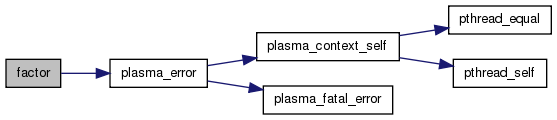
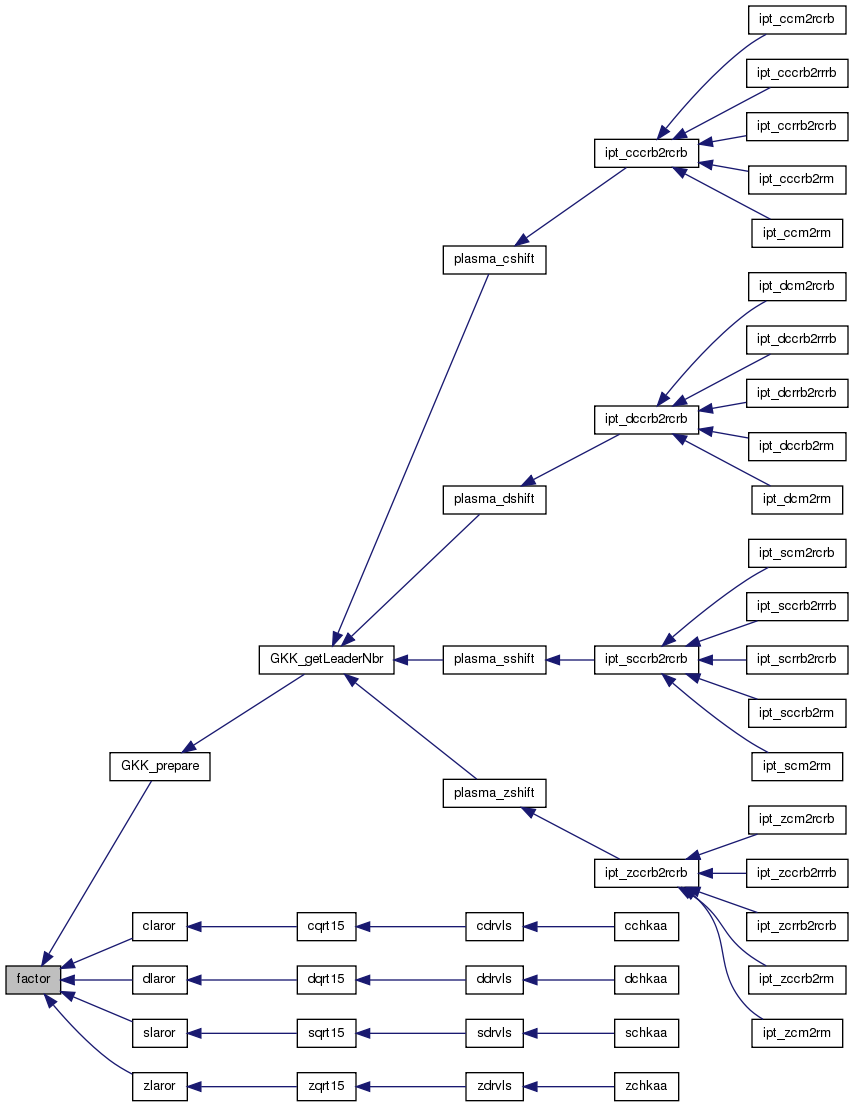
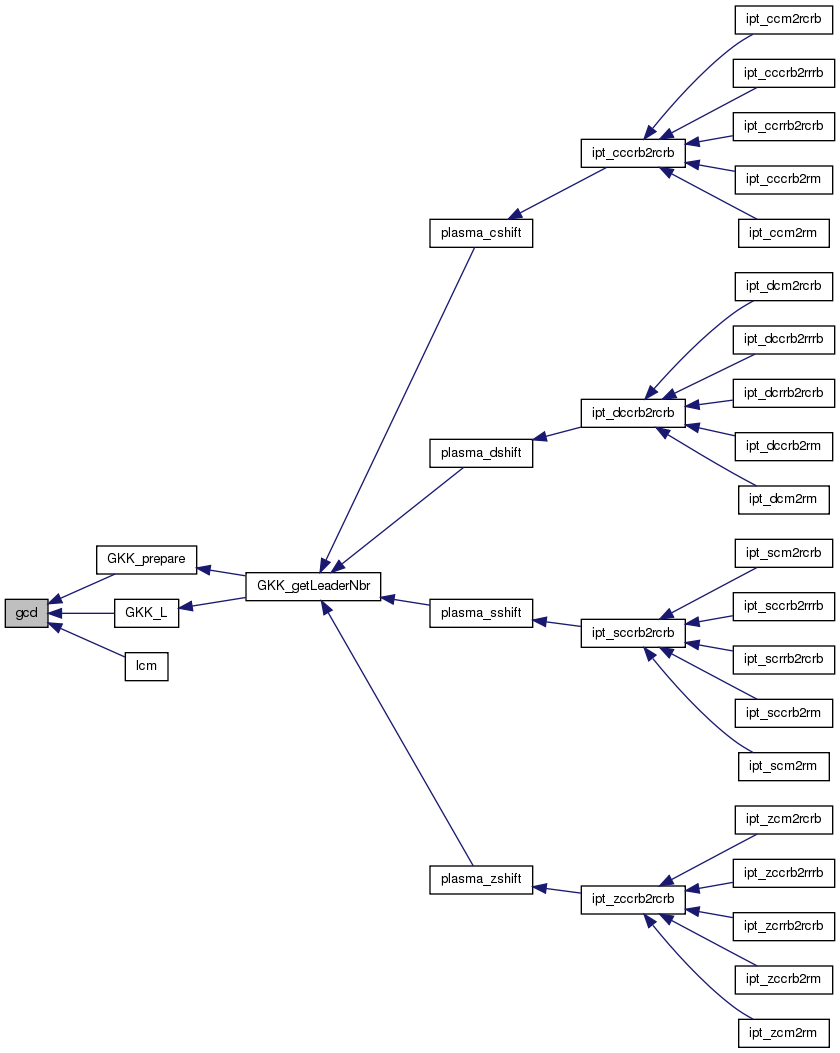
factor Factors an integer into a product of prime powers.

Parameters:

[in]	n
[out]	pr	Array of size PRIME_MAXSIZE On exit, contains the prime factor of n modulo m
[out]	nf	Number of prime factor in n.

Definition at line 748 of file primes.c.

References primedec::e, lapack_testing::f, primedec::p, primedec::pe, plasma_error(), PRIME_MAXSIZE, primes, and PRIMESTABLE_SIZE.

                                            {

    int x, i, f, sqrtx, lnf;

    lnf = 0;
    x  = n;
    sqrtx = (int)sqrt((double)x);
    i  = 0;
    f  = 1;
    while( x > 1 ) {
        /* Get a prime f */
        f = primes[i];
        
        /* check if x is prime */
        if( f > sqrtx ) {
            if( lnf > PRIME_MAXSIZE ) {
                plasma_error(__func__, "input matrix pr has too few columns");
            }
            
            pr[lnf].p  = x;
            pr[lnf].e  = 1;
            pr[lnf].pe = x;
            lnf++;
            break;
        }

        /* check if f | x */
        if( (x % f) == 0 ) {
            /* found a new prime factor of x, namely f */
            if( lnf > PRIME_MAXSIZE ) {
              plasma_error(__func__, "input matrix pr has too few columns");
            }
            pr[lnf].p  = f;
            pr[lnf].e  = 1;
            pr[lnf].pe = f;

            x = x / f;
            while( (x % f) == 0 ) {
                x = x / f;
                pr[lnf].e  += 1;
                pr[lnf].pe *= f;
            }
            sqrtx = (int)sqrt((double)x);
            lnf++;
        }
        
        i++;
        if( !(i < PRIMESTABLE_SIZE) ) {
            plasma_error(__func__, "ran out of table");
        }
    }
    *nf = lnf;
}

Here is the call graph for this function:

Here is the caller graph for this function:

int gcd	(	int	a,
		int	b
	)

---

gcd computes the greatest common divisor of a and b.

Parameters:

[in]	a
[in]	b

Returns:

Return values:

the	greatest common divisor of a and b.

Definition at line 673 of file primes.c.

                     {
    int x, y, t;
    x = a;
    y = b;
    while( y != 0 ) {
        t = y;
        y = x%y;
        x = t;
    }
    return x;
}

Here is the caller graph for this function:

int lcm	(	int	a,
		int	b
	)

---

lcm computes the least common mutliple of a and b

Parameters:

[in]	a
[in]	b

Returns:

Return values:

the	least common multiple of a and b

Definition at line 651 of file primes.c.

References gcd().

                      {
    return (a / gcd(a, b)) * b;
}

Here is the call graph for this function:

int64_t maxval	(	int	n,
		int *	T
	)

---

maxval return the maximum value found in T

Parameters:

[in]	n	Size of the array T
[in]	T	Array of integers of size n

Returns:

Return values:

the	maximum found in T

Definition at line 857 of file primes.c.

References max.

                              {
    int64_t max = T[0];
    int i;
    
    for (i=1; i<n; i++) {
        if (T[i] > max)
            max = T[i];
    }
    return max;
}

Here is the caller graph for this function:

int minloc	(	int	n,
		int *	T
	)

---

minloc return the indice of the minimum in array T

Parameters:

[in]	n	Size of the array T
[in]	T	Array of integers of size n

Returns:

Return values:

the	indice of the minimum in T

Definition at line 823 of file primes.c.

                          {
    int mini = 0; 
    int minT = T[0];
    int i;
    
    for (i=1; i<n; i++) {
        if (T[i] < minT) {
            minT = T[i];
            mini = i;
        }
    }
    return mini;
}

Here is the caller graph for this function:

int modpow	(	int	x,
		int	n,
		int	m
	)

---

modpow computes the modular power x^n mod m using recursive squaring. The number of operations is proportional to the logarithm of the exponent n.

Parameters:

[in]	x
[in]	n
[in]	m

Returns:

Return values:

the	modular power x^n mod m

Definition at line 707 of file primes.c.

                                {
    int64_t Nn, y, z, t;

    if( n == 0 )
        return 1;

    Nn = n;
    y  = 1;
    z  = x;

    while (1) {
        t  = Nn % 2;
        Nn = Nn / 2;
        if( t != 0 ) {
            y = (z*y) % m;
            if( Nn == 0 )
              return y;
        }
        z = (z * z) % m;
    }
}

Here is the caller graph for this function:

int64_t sum	(	int	n,
		int *	T
	)

---

sum return the sum(T[i], i=0..n-1)

Parameters:

[in]	n	Size of the array T
[in]	T	Array of integers of size n

Returns:

Return values:

sum(T[i],i=0..n-1)

Definition at line 888 of file primes.c.

References sum().

                           {
    int64_t sum = T[0];
    int i;
    
    for (i=1; i<n; i++)
      sum += T[i];

    return sum;
}

Here is the call graph for this function:

Here is the caller graph for this function:

---

Variable Documentation

int primes[PRIMESTABLE_SIZE]

Definition at line 30 of file primes.c.