example_sgelqf.c File Reference

Example using LQ factorization. More...

#include <stdlib.h>
#include <stdio.h>
#include <string.h>
#include <math.h>
#include <plasma.h>
#include <cblas.h>
#include <lapacke.h>
#include <core_blas.h>

Include dependency graph for example_sgelqf.c:

Go to the source code of this file.

Macros
#define	max(a, b)   ((a) > (b) ? (a) : (b))
#define	min(a, b)   ((a) < (b) ? (a) : (b))

Functions
int	check_orthogonality (int, int, int, float *)
int	check_factorization (int, int, float *, float *, int, float *)
int	main ()

Variables
int	IONE = 1
int	ISEED [4] = {0,0,0,1}

---

Detailed Description

Example using LQ factorization.

PLASMA testing routines PLASMA is a software package provided by Univ. of Tennessee, Univ. of California Berkeley and Univ. of Colorado Denver

Version:

2.4.5

Author:

Bilel Hadri

Date:

2010-11-15 s Tue Nov 22 14:35:52 2011

Definition in file example_sgelqf.c.

---

Macro Definition Documentation

#define max	(		a,
			b
	)		((a) > (b) ? (a) : (b))

Definition at line 28 of file example_sgelqf.c.

#define min	(		a,
			b
	)		((a) < (b) ? (a) : (b))

Definition at line 31 of file example_sgelqf.c.

---

Function Documentation

int check_factorization	(	int	M,
		int	N,
		float *	A1,
		float *	A2,
		int	LDA,
		float *	Q
	)

Definition at line 157 of file example_sgelqf.c.

References cblas_sgemm(), CblasColMajor, CblasNoTrans, L, lapack_const, max, and PlasmaInfNorm.

{
    float Anorm, Rnorm;
    float alpha, beta;
    int info_factorization;
    int i,j;
    float eps;

    eps = LAPACKE_slamch_work('e');

    float *Ql       = (float *)malloc(M*N*sizeof(float));
    float *Residual = (float *)malloc(M*N*sizeof(float));
    float *work              = (float *)malloc(max(M,N)*sizeof(float));

    alpha=1.0;
    beta=0.0;

    if (M >= N) {
        /* Extract the R */
        float *R = (float *)malloc(N*N*sizeof(float));
        memset((void*)R, 0, N*N*sizeof(float));
        LAPACKE_slacpy_work(LAPACK_COL_MAJOR,'u', M, N, A2, LDA, R, N);

        /* Perform Ql=Q*R */
        memset((void*)Ql, 0, M*N*sizeof(float));
        cblas_sgemm(CblasColMajor, CblasNoTrans, CblasNoTrans, M, N, N, (alpha), Q, LDA, R, N, (beta), Ql, M);
        free(R);
    }
    else {
        /* Extract the L */
        float *L = (float *)malloc(M*M*sizeof(float));
        memset((void*)L, 0, M*M*sizeof(float));
        LAPACKE_slacpy_work(LAPACK_COL_MAJOR,'l', M, N, A2, LDA, L, M);

    /* Perform Ql=LQ */
        memset((void*)Ql, 0, M*N*sizeof(float));
        cblas_sgemm(CblasColMajor, CblasNoTrans, CblasNoTrans, M, N, M, (alpha), L, M, Q, LDA, (beta), Ql, M);
        free(L);
    }

    /* Compute the Residual */
    for (i = 0; i < M; i++)
        for (j = 0 ; j < N; j++)
            Residual[j*M+i] = A1[j*LDA+i]-Ql[j*M+i];

    Rnorm = LAPACKE_slange_work(LAPACK_COL_MAJOR, lapack_const(PlasmaInfNorm), M, N, Residual, M, work);
    Anorm = LAPACKE_slange_work(LAPACK_COL_MAJOR, lapack_const(PlasmaInfNorm), M, N, A2, LDA, work);

    if (M >= N) {
        printf("============\n");
        printf("Checking the QR Factorization \n");
        printf("-- ||A-QR||_oo/(||A||_oo.N.eps) = %e \n",Rnorm/(Anorm*N*eps));
    }
    else {
        printf("============\n");
        printf("Checking the LQ Factorization \n");
        printf("-- ||A-LQ||_oo/(||A||_oo.N.eps) = %e \n",Rnorm/(Anorm*N*eps));
    }

    if (isnan(Rnorm / (Anorm * N *eps)) || (Rnorm / (Anorm * N * eps) > 10.0) ) {
        printf("-- Factorization is suspicious ! \n");
        info_factorization = 1;
    }
    else {
        printf("-- Factorization is CORRECT ! \n");
        info_factorization = 0;
    }

    free(work); free(Ql); free(Residual);

    return info_factorization;
}

Here is the call graph for this function:

int check_orthogonality	(	int	M,
		int	N,
		int	LDQ,
		float *	Q
	)

Definition at line 107 of file example_sgelqf.c.

References cblas_ssyrk(), CblasColMajor, CblasNoTrans, CblasTrans, CblasUpper, lapack_const, min, and PlasmaInfNorm.

{
    float alpha, beta;
    float normQ;
    int info_ortho;
    int i;
    int minMN = min(M, N);
    float eps;
    float *work = (float *)malloc(minMN*sizeof(float));

    eps = LAPACKE_slamch_work('e');
    alpha = 1.0;
    beta  = -1.0;

    /* Build the idendity matrix USE DLASET?*/
    float *Id = (float *) malloc(minMN*minMN*sizeof(float));
    memset((void*)Id, 0, minMN*minMN*sizeof(float));
    for (i = 0; i < minMN; i++)
        Id[i*minMN+i] = (float)1.0;

    /* Perform Id - Q'Q */
    if (M >= N)
        cblas_ssyrk(CblasColMajor, CblasUpper, CblasTrans, N, M, alpha, Q, LDQ, beta, Id, N);
    else
        cblas_ssyrk(CblasColMajor, CblasUpper, CblasNoTrans, M, N, alpha, Q, LDQ, beta, Id, M);

    normQ = LAPACKE_slansy_work(LAPACK_COL_MAJOR, lapack_const(PlasmaInfNorm), 'u', minMN, Id, minMN, work);

    printf("============\n");
    printf("Checking the orthogonality of Q \n");
    printf("||Id-Q'*Q||_oo / (N*eps) = %e \n",normQ/(minMN*eps));

    if ( isnan(normQ / (minMN * eps)) || (normQ / (minMN * eps) > 10.0) ) {
        printf("-- Orthogonality is suspicious ! \n");
        info_ortho=1;
    }
    else {
        printf("-- Orthogonality is CORRECT ! \n");
        info_ortho=0;
    }

    free(work); free(Id);

    return info_ortho;
}

Here is the call graph for this function:

int main

(

)

Definition at line 40 of file example_sgelqf.c.

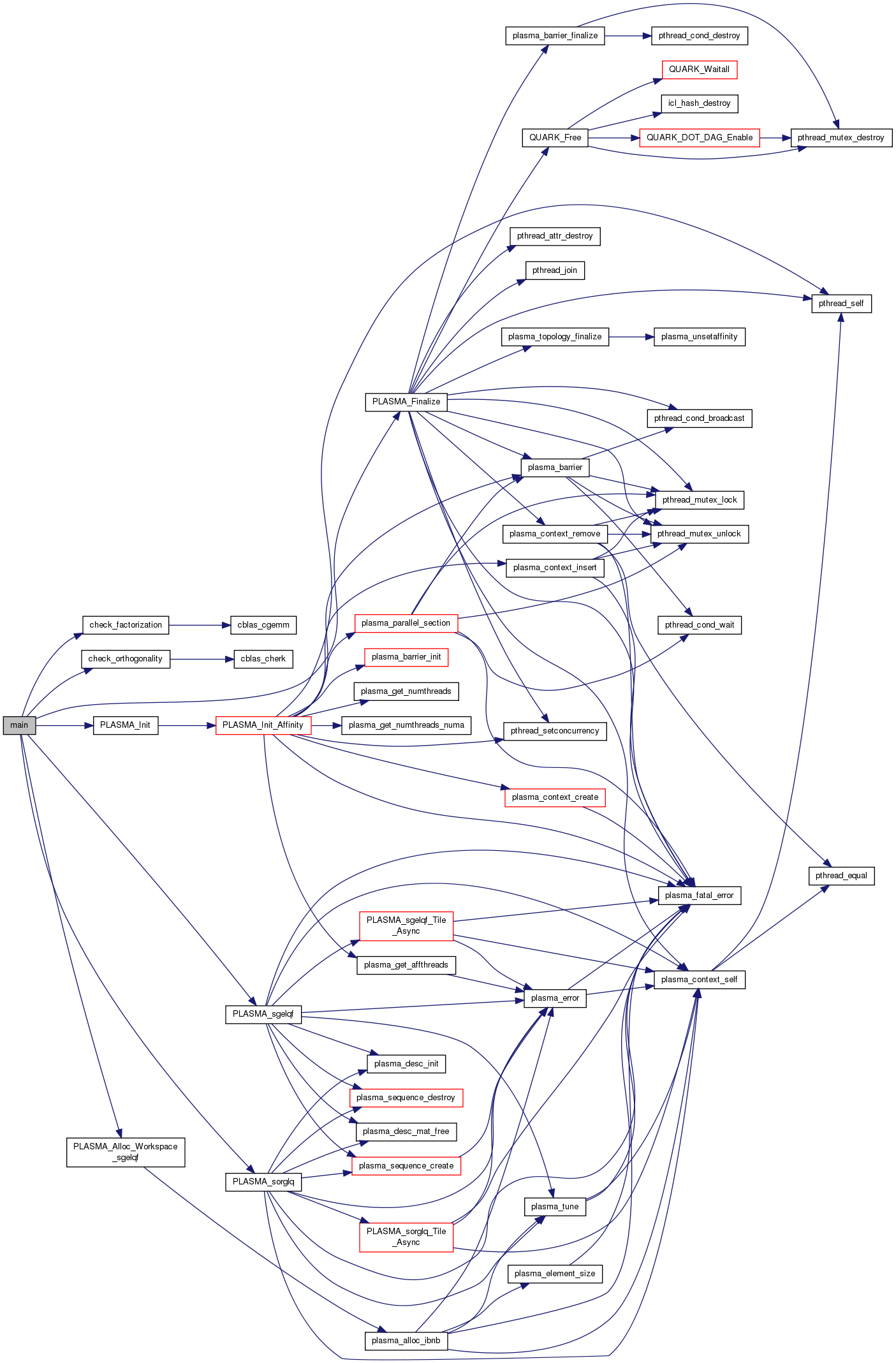
References check_factorization(), check_orthogonality(), IONE, ISEED, min, PLASMA_Alloc_Workspace_sgelqf(), PLASMA_Finalize(), PLASMA_Init(), PLASMA_sgelqf(), PLASMA_sorglq(), Q, and T.

{

    int cores = 2;
    int M     = 10;
    int N     = 15;
    int LDA   = 10;
    int K = min(M, N);
    int info;
    int info_ortho, info_factorization;
    int i,j;
    int LDAxN = LDA*N;

    float *A1 = (float *)malloc(LDA*N*sizeof(float));
    float *A2 = (float *)malloc(LDA*N*sizeof(float));
    float *Q  = (float *)malloc(LDA*N*sizeof(float));
    float *T;

    /* Check if unable to allocate memory */
    if ((!A1)||(!A2)||(!Q)){
        printf("Out of Memory \n ");
        return EXIT_SUCCESS;
    }

    /* Plasma Initialization */
    PLASMA_Init(cores);
    printf("-- PLASMA is initialized to run on %d cores. \n",cores);

    /* Allocate T */
    PLASMA_Alloc_Workspace_sgelqf(M, N, &T);

    /* Initialize A1 and A2 */
    LAPACKE_slarnv_work(IONE, ISEED, LDAxN, A1);
    for (i = 0; i < M; i++)
        for (j = 0; j < N; j++)
            A2[LDA*j+i] = A1[LDA*j+i] ;

    /* Factorization QR of the matrix A2 */
    info = PLASMA_sgelqf(M, N, A2, LDA, T);

    /* Building the economy-size Q */
    memset((void*)Q, 0, LDA*N*sizeof(float));
    for (i = 0; i < K; i++)
        Q[LDA*i+i] = 1.0;

    PLASMA_sorglq(M, N, K, A2, LDA, T, Q, LDA);

    /* Check the orthogonality, factorization and the solution */
    info_ortho = check_orthogonality(M, N, LDA, Q);
    info_factorization = check_factorization(M, N, A1, A2, LDA, Q);

    if ((info_ortho != 0)|(info_factorization != 0)|(info != 0))
       printf("-- Error in SGELQF example ! \n");
    else
       printf("-- Run of SGELQF example successful ! \n");

    free(A1); free(A2); free(Q); free(T);

    PLASMA_Finalize();

    return EXIT_SUCCESS;
}

Here is the call graph for this function:

---

Variable Documentation

int IONE = 1

Definition at line 37 of file example_sgelqf.c.

int ISEED[4] = {0,0,0,1}

Definition at line 38 of file example_sgelqf.c.