#include <lapacke.h>
#include "common.h"

Include dependency graph for core_stsqrt.c:

Macros
#define	REAL

Functions
int	CORE_stsqrt (int M, int N, int IB, float A1, int LDA1, float A2, int LDA2, float T, int LDT, float TAU, float *WORK)
void	QUARK_CORE_stsqrt (Quark quark, Quark_Task_Flags task_flags, int m, int n, int ib, int nb, float A1, int lda1, float A2, int lda2, float *T, int ldt)
void	CORE_stsqrt_quark (Quark *quark)

Detailed Description

PLASMA core_blas kernel PLASMA is a software package provided by Univ. of Tennessee, Univ. of California Berkeley and Univ. of Colorado Denver

Version:: 2.4.5

Author:: Hatem Ltaief; Mathieu Faverge; Jakub Kurzak

Date:: 2010-11-15 s Tue Nov 22 14:35:17 2011

Definition in file core_stsqrt.c.

Macro Definition Documentation

#define REAL

Definition at line 20 of file core_stsqrt.c.

Function Documentation

int CORE_stsqrt	(	int	M,
		int	N,
		int	IB,
		float *	A1,
		int	LDA1,
		float *	A2,
		int	LDA2,
		float *	T,
		int	LDT,
		float *	TAU,
		float *	WORK
	)

CORE_stsqrt computes a QR factorization of a rectangular matrix formed by coupling a complex N-by-N upper triangular tile A1 on top of a complex M-by-N tile A2:

| A1 | = Q * R | A2 |

Parameters:

[in]	M	The number of columns of the tile A2. M >= 0.
[in]	N	The number of rows of the tile A1. The number of columns of the tiles A1 and A2. N >= 0.
[in]	IB	The inner-blocking size. IB >= 0.
[in,out]	A1	On entry, the N-by-N tile A1. On exit, the elements on and above the diagonal of the array contain the N-by-N upper trapezoidal tile R; the elements below the diagonal are not referenced.
[in]	LDA1	The leading dimension of the array A1. LDA1 >= max(1,N).
[in,out]	A2	On entry, the M-by-N tile A2. On exit, all the elements with the array TAU, represent the unitary tile Q as a product of elementary reflectors (see Further Details).
[in]	LDA2	The leading dimension of the tile A2. LDA2 >= max(1,M).
[out]	T	The IB-by-N triangular factor T of the block reflector. T is upper triangular by block (economic storage); The rest of the array is not referenced.
[in]	LDT	The leading dimension of the array T. LDT >= IB.
[out]	TAU	The scalar factors of the elementary reflectors (see Further Details).
[out]	WORK

Returns:

Return values:

PLASMA_SUCCESS	successful exit
<0	if -i, the i-th argument had an illegal value

Definition at line 97 of file core_stsqrt.c.

References cblas_saxpy(), cblas_scopy(), cblas_sgemv(), cblas_sger(), cblas_strmv(), CblasColMajor, CORE_stsmqr(), coreblas_error, max, min, PLASMA_SUCCESS, PlasmaLeft, PlasmaNonUnit, PlasmaNoTrans, PlasmaTrans, and PlasmaUpper.

{
    static float zone  = 1.0;
    static float zzero = 0.0;
    float alpha;
    int i, ii, sb;
    /* Check input arguments */
    if (M < 0) {
        coreblas_error(1, "Illegal value of M");
        return -1;
    }
    if (N < 0) {
        coreblas_error(2, "Illegal value of N");
        return -2;
    }
    if (IB < 0) {
        coreblas_error(3, "Illegal value of IB");
        return -3;
    }
    if ((LDA2 < max(1,M)) && (M > 0)) {
        coreblas_error(8, "Illegal value of LDA2");
        return -8;
    }
    /* Quick return */
    if ((M == 0) || (N == 0) || (IB == 0))
        return PLASMA_SUCCESS;
    for(ii = 0; ii < N; ii += IB) {
        sb = min(N-ii, IB);
        for(i = 0; i < sb; i++) {
            /*
             * Generate elementary reflector H( II*IB+I ) to annihilate
             * A( II*IB+I:M, II*IB+I )
             */
            LAPACKE_slarfg_work(M+1, &A1[LDA1*(ii+i)+ii+i], &A2[LDA2*(ii+i)], 1, &TAU[ii+i]);
            if (ii+i+1 < N) {
                /*
                 * Apply H( II*IB+I ) to A( II*IB+I:M, II*IB+I+1:II*IB+IB ) from the left
                 */
                alpha = -(TAU[ii+i]);
                cblas_scopy(
                    sb-i-1,
                    &A1[LDA1*(ii+i+1)+(ii+i)], LDA1,
                    WORK, 1);
#ifdef COMPLEX
                LAPACKE_slacgv_work(sb-i-1, WORK, 1);
#endif
                cblas_sgemv(
                    CblasColMajor, (CBLAS_TRANSPOSE)PlasmaTrans,
                    M, sb-i-1,
                    (zone), &A2[LDA2*(ii+i+1)], LDA2,
                    &A2[LDA2*(ii+i)], 1,
                    (zone), WORK, 1);
#ifdef COMPLEX
                LAPACKE_slacgv_work(sb-i-1, WORK, 1 );
#endif
                cblas_saxpy(
                    sb-i-1, (alpha),
                    WORK, 1,
                    &A1[LDA1*(ii+i+1)+ii+i], LDA1);
#ifdef COMPLEX
                LAPACKE_slacgv_work(sb-i-1, WORK, 1 );
#endif
                cblas_sger(
                    CblasColMajor, M, sb-i-1, (alpha),
                    &A2[LDA2*(ii+i)], 1,
                    WORK, 1,
                    &A2[LDA2*(ii+i+1)], LDA2);
            }
            /*
             * Calculate T
             */
            alpha = -TAU[ii+i];
            cblas_sgemv(
                CblasColMajor, (CBLAS_TRANSPOSE)PlasmaTrans, M, i,
                (alpha), &A2[LDA2*ii], LDA2,
                &A2[LDA2*(ii+i)], 1,
                (zzero), &T[LDT*(ii+i)], 1);
            cblas_strmv(
                CblasColMajor, (CBLAS_UPLO)PlasmaUpper,
                (CBLAS_TRANSPOSE)PlasmaNoTrans, (CBLAS_DIAG)PlasmaNonUnit, i,
                &T[LDT*ii], LDT,
                &T[LDT*(ii+i)], 1);
            T[LDT*(ii+i)+i] = TAU[ii+i];
        }
        if (N > ii+sb) {
            CORE_stsmqr(
                PlasmaLeft, PlasmaTrans,
                sb, N-(ii+sb), M, N-(ii+sb), IB, IB,
                &A1[LDA1*(ii+sb)+ii], LDA1,
                &A2[LDA2*(ii+sb)], LDA2,
                &A2[LDA2*ii], LDA2,
                &T[LDT*ii], LDT,
                WORK, sb);
        }
    }
    return PLASMA_SUCCESS;
}

Here is the call graph for this function:

Here is the caller graph for this function:

void CORE_stsqrt_quark ( Quark * quark )

Definition at line 238 of file core_stsqrt.c.

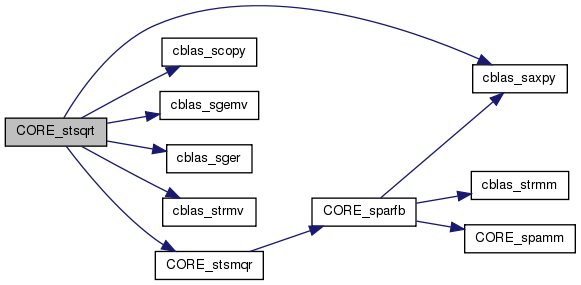
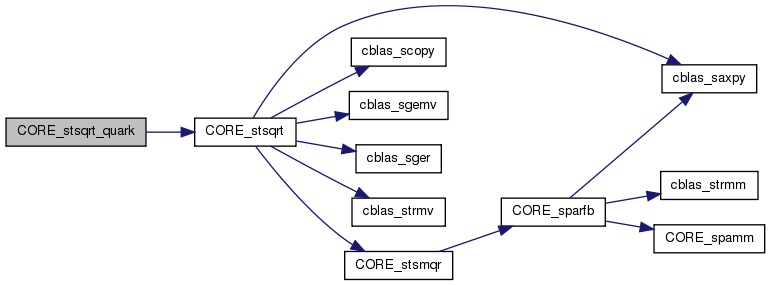
References CORE_stsqrt(), quark_unpack_args_11, T, and TAU.

{
    int m;
    int n;
    int ib;
    float *A1;
    int lda1;
    float *A2;
    int lda2;
    float *T;
    int ldt;
    float *TAU;
    float *WORK;
    quark_unpack_args_11(quark, m, n, ib, A1, lda1, A2, lda2, T, ldt, TAU, WORK);
    CORE_stsqrt(m, n, ib, A1, lda1, A2, lda2, T, ldt, TAU, WORK);
}

Here is the call graph for this function:

Here is the caller graph for this function:

void QUARK_CORE_stsqrt	(	Quark *	quark,
		Quark_Task_Flags *	task_flags,
		int	m,
		int	n,
		int	ib,
		int	nb,
		float *	A1,
		int	lda1,
		float *	A2,
		int	lda2,
		float *	T,
		int	ldt
	)

Definition at line 209 of file core_stsqrt.c.

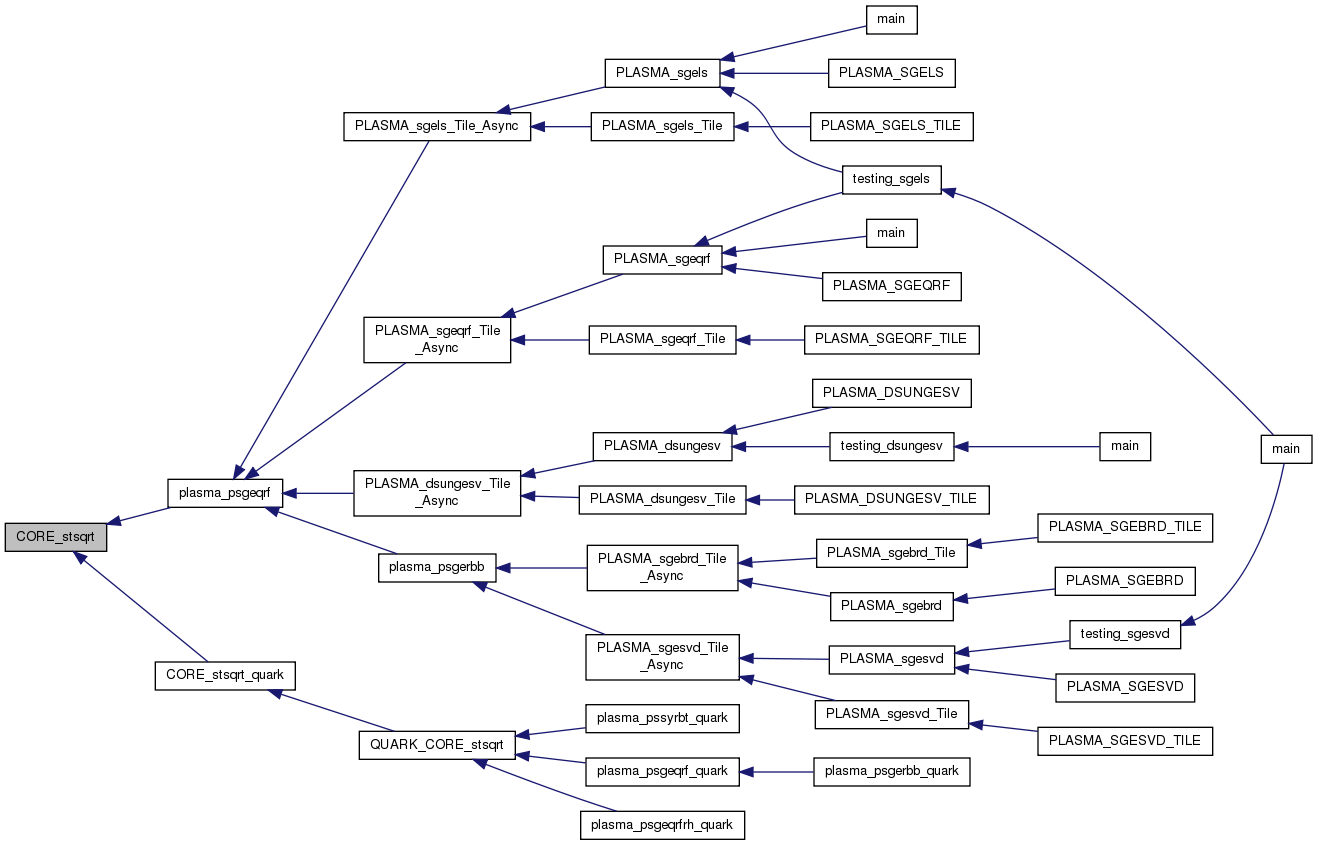
References CORE_stsqrt_quark(), DAG_CORE_TSQRT, INOUT, LOCALITY, OUTPUT, QUARK_Insert_Task(), QUARK_REGION_D, QUARK_REGION_U, SCRATCH, and VALUE.

{
    DAG_CORE_TSQRT;
    QUARK_Insert_Task(quark, CORE_stsqrt_quark, task_flags,
        sizeof(int),                        &m,     VALUE,
        sizeof(int),                        &n,     VALUE,
        sizeof(int),                        &ib,    VALUE,
        sizeof(float)*nb*nb,    A1,            INOUT | QUARK_REGION_D | QUARK_REGION_U,
        sizeof(int),                        &lda1,  VALUE,
        sizeof(float)*nb*nb,    A2,            INOUT | LOCALITY,
        sizeof(int),                        &lda2,  VALUE,
        sizeof(float)*ib*nb,    T,             OUTPUT,
        sizeof(int),                        &ldt,   VALUE,
        sizeof(float)*nb,       NULL,          SCRATCH,
        sizeof(float)*ib*nb,    NULL,          SCRATCH,
        0);
}

Here is the call graph for this function:

Here is the caller graph for this function:

Macros

Functions

Detailed Description

Macro Definition Documentation

Function Documentation