The scalable data generator constructs a list of edge tuples containing vertex identifiers, and randomly-selected positive integers are assigned as weights on the edges of the graph. Each edge is directed from the first vertex of its tuple to the second. The generated list of tuples must not exhibit any locality that can be exploited by the computational kernels. For generating the graphs, we use a synthetic graph model that matches the topologies seen in real-world applications: the Recursive MATrix (R-MAT) scale-free graph generation algorithm.19 For ease of discussion, the description of this R-MAT generator uses an adjacency matrix data structure; however, implementations may use any alternate approach that outputs the equivalent list of edge tuples. The R-MAT model recursively sub-divides the adjacency matrix of the graph into four equal-sized partitions and distributes edges within these partitions with unequal probabilities. Initially, the adjacency matrix is empty and edges are added one at a time. Each edge chooses one of the four partitions with probabilities a, b, c, and d, respectively. At each stage of the recursion, the parameters are varied slightly and renormalized. For simplicity in this SSCA, multiple edges, self-loops, and isolated vertices, may be ignored in the subsequent kernels. The algorithm also generates the data tuples with high degrees of locality. Thus, as a final step, vertex numbers must be randomly permuted, and then edge tuples randomly shuffled.
This kernel constructs the graph from the data generator output tuple list. The graph can be represented in any manner, but cannot be modified by subsequent kernels. The number of vertices in the graph is not provided and needs to be determined in this kernel.
The intent of this kernel is to examine all edge weights to determine those vertex pairs with the largest integer weight. The output of this kernel will be an edge list, S, that will be saved for use in the following kernel.
Starting from vertex pairs in the set S, this kernel produces subgraphs that consist of the vertices and edges along all paths of length less than subGrEdgeLength, an input parameter. A possible algorithm for graph extraction is Breadth-First Search.
This kernel identifies the set of vertices in the graph with the highest betweenness centrality score. Betweenness Centrality is a shortest paths, enumeration-based centrality metric introduced by Freeman.20 This is done using a betweenness centrality algorithm that computes this metric for every vertex in the graph. Let σst denote the number of shortest paths between vertices s and t, and σst(v) denote the number of paths passing through v. Betweenness centrality of a vertex v is defined as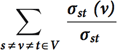 
. The output
of this kernel is a betweenness centrality score for each vertex in the graph and the set of vertices with the highest betweenness centrality score.
For kernel 4, we filter out a fraction of edges using a filter described in the written specification. Because of the high computation cost of kernel 4, an exact implementation considers all vertices as starting points in the betweenness centrality metric, while an approximate implementation uses a subset of starting vertices (VS).
A straightforward way of computing betweenness vertex would be as follows:
- Compute the length and number of shortest paths between all pairs (s, t).
- For each vertex v, calculate the summation of all possible pair-wise dependencies
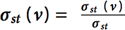
Recently, Brandes21 proposed a faster algorithm that computes the exact betweenness centrality score for all vertices in the graph. Brandes noted that it is possible to augment Dijkstra’s single-source shortest paths (SSSP) algorithm (for weight graphs) and breadth-first search (BFS) for unweighted graphs to compute the dependencies. Bader and Madduri give the first parallel betweenness centrality algorithm in [22].
In order to compare the performance of SSCA #2 Version 2.x kernel 4 implementations across a variety of architectures, programming models, and productivity languages and frameworks, as well as normalizing across both exact and approximate implementations, we adopt a new performance metric, a rate called traversed edges per second (TEPS).
