testing_ssygv.c File Reference

#include <stdlib.h>
#include <stdio.h>
#include <string.h>
#include <math.h>
#include <plasma.h>
#include <cblas.h>
#include <lapacke.h>
#include <core_blas.h>
#include "testing_smain.h"

Include dependency graph for testing_ssygv.c:

Go to the source code of this file.

Macros
#define	REAL

Functions
int	testing_ssygv (int argc, char **argv)

---

Detailed Description

PLASMA testing routines PLASMA is a software package provided by Univ. of Tennessee, Univ. of California Berkeley and Univ. of Colorado Denver

Version:

2.4.5

Author:

Hatem Ltaief

Date:

2010-11-15 s Tue Nov 22 14:35:49 2011

Definition in file testing_ssygv.c.

---

Macro Definition Documentation

#define REAL

Definition at line 27 of file testing_ssygv.c.

---

Function Documentation

int testing_ssygv	(	int	argc,
		char **	argv
	)

Definition at line 36 of file testing_ssygv.c.

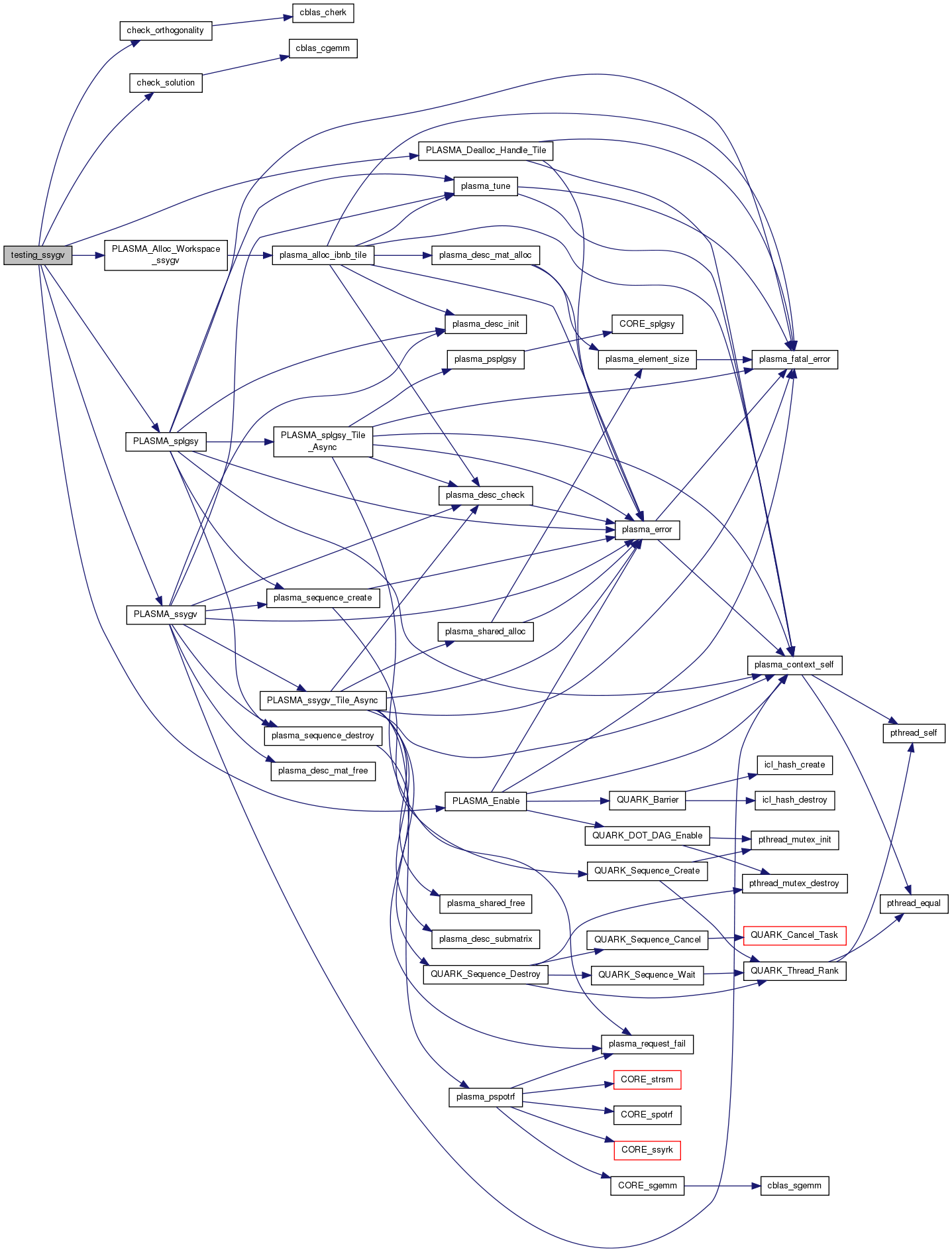
References check_orthogonality(), check_solution(), itype, itypestr, lapack_const, PLASMA_Alloc_Workspace_ssygv(), PLASMA_Dealloc_Handle_Tile(), PLASMA_Enable(), PLASMA_ERRORS, PLASMA_splgsy(), PLASMA_ssygv(), PLASMA_WARNINGS, PlasmaNoVec, PlasmaVec, Q, T, uplo, uplostr, and USAGE.

{
    /* Check for number of arguments*/
    if (argc != 3) {
        USAGE("HEGV", "N LDA LDB",
              "   - N    : size of the matrices A and B\n"
              "   - LDA  : leading dimension of the matrix A\n"
              "   - LDB  : leading dimension of the matrix B\n");
        return -1;
    }

    float      eps = LAPACKE_slamch_work('e');
    PLASMA_enum vec = PlasmaNoVec;
    int    N        = atoi(argv[0]);
    int    LDA      = atoi(argv[1]);
    int    LDB      = atoi(argv[2]);
    int    LDQ      = LDA;
    int    LDAxN    = LDA*N;
    int    LDBxN    = LDB*N;
    int    LDQxN    = LDQ*N;

    int info_ortho     = 0;
    int info_solution  = 0;
    int info_reduction = 0;
    int i, u;

    float *A1    = (float *)malloc(LDAxN*sizeof(float));
    float *A2    = (float *)malloc(LDAxN*sizeof(float));
    float *B1    = (float *)malloc(LDBxN*sizeof(float));
    float *B2    = (float *)malloc(LDBxN*sizeof(float));
    float *Q     = (float *)malloc(LDQxN*sizeof(float));
    float *Ainit = (float *)malloc(LDAxN*sizeof(float));
    float *Binit = (float *)malloc(LDBxN*sizeof(float));
    float *W1 = (float *)malloc(N*sizeof(float));
    float *W2 = (float *)malloc(N*sizeof(float));
    float *work = (float *)malloc(3*N* sizeof(float));
    PLASMA_desc *T;

    /* Check if unable to allocate memory */
    if ((!A1)||(!A2)||(!B1)||(!B2)||(!Q)||(!Ainit)||(!Binit)){
        printf("Out of Memory \n ");
        return -2;
    }

    /*
    PLASMA_Disable(PLASMA_AUTOTUNING);
    PLASMA_Set(PLASMA_TILE_SIZE, 120);
    PLASMA_Set(PLASMA_INNER_BLOCK_SIZE, 20);
    */
    
    PLASMA_Enable(PLASMA_WARNINGS);
    PLASMA_Enable(PLASMA_ERRORS);
    PLASMA_Alloc_Workspace_ssygv(N, N, &T);

    /*----------------------------------------------------------
    *  TESTING SSYGV
    */

    /* Initialize A1 and Ainit */
    PLASMA_splgsy(0., N, A1, LDA, 5198);
    LAPACKE_slacpy_work(LAPACK_COL_MAJOR, 'A', N, N, A1, LDA, Ainit, LDA);

    /* Initialize B1 and Binit */
    PLASMA_splgsy((float)N, N, B1, LDB, 4321 );
    LAPACKE_slacpy_work(LAPACK_COL_MAJOR, 'A', N, N, B1, LDB, Binit, LDB);

    printf("\n");
    printf("------ TESTS FOR PLASMA SSYGV ROUTINE -------  \n");
    printf("        Size of the Matrix %d by %d\n", N, N);
    printf("\n");
    printf(" The matrix A is randomly generated for each test.\n");
    printf("============\n");
    printf(" The relative machine precision (eps) is to be %e \n",eps);
    printf(" Computational tests pass if scaled residuals are less than 60.\n");

    /*----------------------------------------------------------
     *  TESTING SSYGV
     */

    for (i=0; i<3; i++) {
        for (u=0; u<2; u++) {
            LAPACKE_slaset_work(LAPACK_COL_MAJOR, 'A', LDA, N, 0., 1., Q, LDA);

            memcpy(A2, Ainit, LDAxN*sizeof(float));
            memcpy(B2, Binit, LDBxN*sizeof(float));

            PLASMA_ssygv(itype[i], vec, uplo[u], N, A2, LDA, B2, LDB, W2, T, Q, LDQ);

            /* Check the orthogonality, reduction and the eigen solutions */
            if (vec == PlasmaVec)
                info_ortho = check_orthogonality(N, N, Q, LDA, eps);
            /* 
             * WARNING: For now, Q is associated to Band tridiagonal reduction and 
             * not to the final tridiagonal reduction, so we can not call the check
             */
            if (0)
                info_reduction = check_reduction(itype[i], uplo[u], N, 1, A1, A2, LDA, B2, LDB, Q, eps);

            memcpy(A1, Ainit, LDAxN*sizeof(float));
            memcpy(B1, Binit, LDBxN*sizeof(float));

            LAPACKE_ssygv( LAPACK_COL_MAJOR, 
                     itype[i], lapack_const(vec), lapack_const(uplo[u]),
                     N, A1, LDA, B1, LDB, W1);

            /*info_solution  = check_solution(N, N, N, A1, LDA, B1, B2, LDB, eps);*/
            info_solution = check_solution(N, W1, W2, eps);
         
            if ( (info_ortho == 0) & (info_reduction == 0) & (info_solution == 0)) {
                printf("***************************************************\n");
                printf(" ---- TESTING SSYGV (%s, %s) ...................... PASSED !\n", itypestr[i], uplostr[u]);
                printf("***************************************************\n");
            }
            else {
                printf("************************************************\n");
                printf(" - TESTING SSYGV (%s, %s) ... FAILED !\n", itypestr[i], uplostr[u]);
                printf("************************************************\n");
            } 
        }
    }

    PLASMA_Dealloc_Handle_Tile(&T);
    free(A1); 
    free(A2); 
    free(B1); 
    free(B2); 
    free(Q); 
    free(Ainit); 
    free(Binit); 
    free(W1);
    free(W2);
    free(work);

    return 0;
}

Here is the call graph for this function:

Here is the caller graph for this function: