
November 2006 B
|
A Compiler-guided Instrumentation for Application Behavior Understanding
|
 November 2006 B |
The standard approach to the problem of application behavior understanding relies on instruction-level instrumentation. This approach generates humongous volumes of data that overwhelm programmers in trying to understand the cause-effect relationships in their applications and thus improve the performance of their codes. This article describes an integrated compiler and run-time approach that allows the extraction of relevant program behavior information by judiciously instrumenting the source code and deriving performance metrics such as range of array reference addresses, array access stride information or data reuse characteristics. This information ultimately allows programmers to understand why the performance is what it is on a given machine as they relate to program constructs that can be reasoned about. We describe the overall organization of our compiler and run-time instrumentation system and present preliminary results for a selected set of kernel codes. The approach allow programmers to derive a wealth of information about the program behavior with a run-time overhead of less than 15% of the original code’s execution time making this attractive to instrument and analysis of code with extremely long running times where binary-level approaches are simply impractical.
Understanding the performance of modern high-performance computing machines has become notoriously difficult. These architectures expose to the programmers different hardware mechanisms that often interact in not so predictable ways. Aiming at improving their performance, programmers must resort to low-level instrumentation techniques, such as binary rewriting, to capture run-time execution data from which they hope to understand the performance behavior of the program. This approach, however, generates huge volumes of raw data at a level of abstraction that is seldom adequate for programmers to relate to the source code of their applications. Programmers are thus left guessing which style of coding is adequate for the compiler and the target architecture at hand. Worse, when one of these two components change, the learning investment is wasted, as the process must be restarted.
In this work we describe an alternative approach that relies on high-level source code instrumentation guided by the application of compiler analyses techniques. The basic idea is to judiciously instrument the application source code to extract various execution metrics that can be related to the source code. While some of the aspects of the compiler-architecture interactions are not directly modeled, the fundamental program behavior is retained at a level of abstraction that allows the compiler to relate the observed metrics to source-level program constructs programmers can understand. An added benefit exists in the isolation of the approach from the compiler effects or idiosyncrasies and thus provides a path for program behavior prediction for future architectures for which a compiler or the actual machines do not yet exist.
Consider as an illustrative example the code in Figure 1. For each invocation of the innermost loop, the computation accesses m elements of the array A with a stride of 1 and m elements of the array B with a stride that is dictated by the array size of B. There are several key observations in this example. First, the accesses to the array A and B are dependent on the range of values n and m which are not known at compile time. Second, the range of addresses to the array A are repeated across the invocations of the i loop. Finally, and although some of the values are not known, such as the actual value of k, its value is not modified throughout the execution of both loops and thus can be safely considered to be loop invariant with respect to these two loops.
|
|
A way to capture the behavior of the program in more detail is to instrument it at the source-code level as shown on the right-hand-side of figure 1. Here we have augmented the original code with calls to instrumentation functions with the appropriate arguments. For instance, saveAddrRange(Ref1,A[k][0],A[k][N-1])will record that, at the particular execution point in the program, the range defined by the two arguments A[k][0],A[k][n-1]will be accessed m times. In this particular instrumentation, we are taking advantage of the fact that the range of addresses is clearly invariant with respect to the i-loop and thus can be hoisted outside the two loops. In this example the loop bounds are symbolically constant and the array access functions are affine with respect to the loop index variables. In the end with the results obtained by this instrumentation, we can learn valuable information regarding the range of addresses the computation accesses and/or the access patterns and thus locality of reference.
Many other authors have addressed the problem of understanding and quantifying the amount of reuse in applications. In the context of scientific application codes, such as the SpecFP benchmark suite, Sherwood et. al. 1 developed a low-level instruction instrumentation approach that identifies the phases of a given computation in terms of the similarities between executed instructions. Other authors have focused on cache locality metrics (e.g., 2 3 4) whereas other use temporal reuse distance or stack distances.5 6 Weinberg et. al.7 have implemented the locality scores described in this document using at a very low-level instrumentation approach.
All these efforts have in common the fact that they instrument the addresses and instruction issued by a running executable directly at a very low-level.8 9 10 11 They offer the promise of high precision, provided one can cope with the enormous data volume they generate or the substantial application slowdown. The approach described in this document explores the opposite end of the instrumentation spectrum. It does not rely on low-level instrumentation, but on high-level source code instrumentation. This approach is faster but comes at a loss in precision, with the additional handicap that it does not take into account the compiler effects – how the compiler has modified the generated code to included hardware-oriented execution transformations such as pre-fetching or speculation. The fundamental premise of this work is that it is possible with little source level instrumentation overhead to capture a large amount of program execution information.
We now describe in more detail the use of compiler analyses and source-level code instrumentation to extract as much information about the program behavior as possible and with the least amount of run-time overhead.
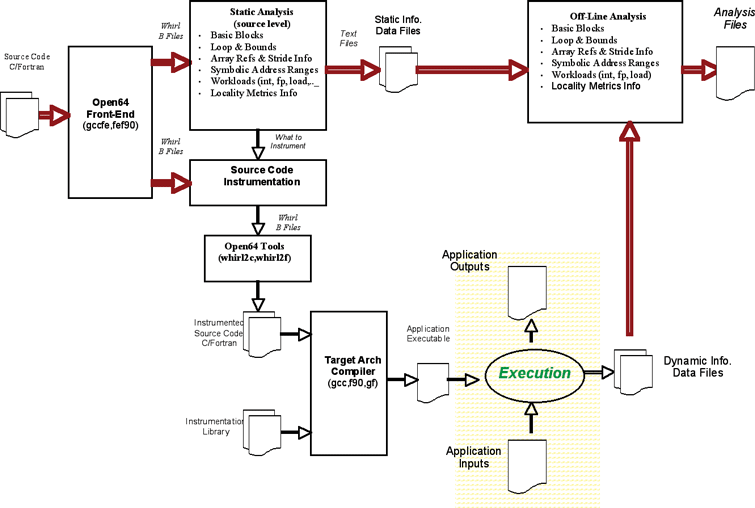
Figure 2 depicts the overall system architecture. We use the Open64 infrastructure for program internal representation and transformation.12 Given a source file, the compiler performs a series of analyses and generates a set of static information files. These files have some of the information about the program structure such as basic blocks and loop organization, and about the program structure the compiler can determine statically. Next, the compiler instruments the source code with library function calls to capture at run-time the missing pieces of information. At run-time the execution collects these missing pieces of information in internal data structures to be output to selected files when the program executes with real input data. These instrumented files are then compiled with the native compiler to generate an executable that is linked against the instrumentation library.
We have implemented the following basic compiler analyses in Open64 that form the basis for our instrumentation:
Using the basic information from these analyses the compiler instruments the code to determine the following program execution properties:
The compiler uses the static information to derive as precise information as possible with as little instrumentation as required. For example, if the loop bounds of a given array are not known at compile time but they depend on variables that do not change through the execution of the loop (i.e., they are symbolically constant), the compiler needs only to capture the value of the bounds once and determine at run-time (with the help of an auxiliary library routine) what the actual bounds are. In extreme cases, however, the compiler may not be able to ascertain if a given expression is symbolically constant, it thus resorts to a very simplistic instrumentation that keeps track of every single loop iteration execution by inserting a counter in the transformed code. The various levels of instrumentation at the source-code level are depicted in figure 3 below.
741: do 10 i = 1, n
742: …
743: 10 continue
740: call SaveLoopBounds(1,n)
741: do 10 i = 1, n
742: …
743: 10 continue
747: do 10 k=c(j),c(j+1)-1
748: …
749: 10 continue
746: call saveLoopBounds(c(j),c(j+1)-1)
747: do 10 k = c(j),c(j+1)-1
748: …
749: 10 continue
747: 100
748: …
749: goto 100
746: call setCurentLoop(loopid)
747: 100 call saveLoopIteration()
748: …
749: goto 100
This instrumentation focuses on capturing metrics at the basic block level. For this reason, the compiler assigns a unique identifier to each basic block, thus allowing a post-processing tool to gather the various basic block metrics and convolve the corresponding execution frequencies and symbolic array information for analysis. Overall, this source level instrumentation is accomplished by the declaration of extra counter variables and library calls whose placement and arguments are determined by the compiler analysis.
As an application of these static and run-time instrumentation techniques, we now describe a specific program behavior model - locality metrics. In particular, we are interested in computing a temporal and spatial locality metric that can quantitatively distinguish between programs with distinct memory access pattern behaviors and thus distinct memory hierarchy performance.
A program will exhibit high spatial locality if it tends to visit memory locations that are close to each other in space. For instance, if a program accesses the data organized as an array with a stride of 1, it exhibits very high spatial locality. If the memory access patterns are very random, its spatial locality is low. Conversely, a program will exhibit a high temporal locality if it tends to repeatedly revisit the same memory locations in a small window of accesses. Given these loose concepts in a computation, we plot the memory access behavior of a computation on a two-dimensional axis normalized between zero and one on both temporal and spatial locality axis as depicted in figure 4. A computation that randomly accesses memory will exhibit both very low spatial and very low temporal locality, and will therefore be plotted in the corner of the diagram close to the origin. A computation that scans an extremely large portion of the memory in a stride 1 array access pattern and that never revisits the same location will have high spatial locality but low temporal locality. On the other hand, a computation that revisits data often and scans the memory using a unit stride, as is the case with common matrix-matrix computations, will exhibit high temporal and spatial localities and thus be close to the (1,1) corner of the diagram. Finally, it is possible to conceive a computation that has very random behavior but revisits the same randomly visited locations often. This computation will have high temporal locality but low spatial locality.
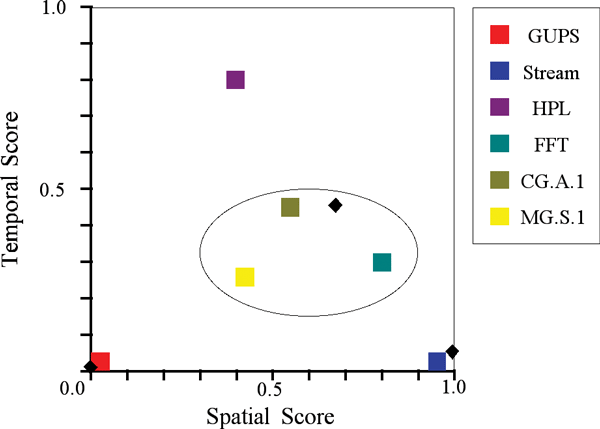
These concepts of spatial and temporal locality have been recently explored by Weinberg et. al.,7 who developed a series of scoring metrics to approximate more rigorous definitions of spatial and temporal locality. The implementation of their spatial and temporal locality scores is very expensive and calls for the analysis of every memory access a computation issues to determine if the specific location has been visited in the past and if so, how long ago. They also classify the various data access streams trying to uncover the stride information as they define a spatial score as a direct function of the stride associated with a given data stream.
In this work, we define two scoring metrics for the spatial and temporal localities of access streams generated by array references. A stream generated by an array reference that traverses a range of addresses from a lower bound (lb) to an upper bound (ub) with stride (st) exhibits a spatial locality of 1/st. Thus a unit stride walk through the elements of an array will correspond to a 1.0 spatial locality scoring and an increasingly longer stride will lead to very low score values. A random scan of the array locations will lead to a spatial score of zero. Intuitively, this model matches the cost model of a cache-supported memory hierarchy, as shorter strides will increase the likelihood of a given data item being on the cache due to the line-size effects. In this work, we use the average stride information that the run-time instrumentation uncovers by using the static and dynamic information to compute a weighted sum over all basic blocks of the spatial locality score, as given below. The weights are simply the relative frequency with which each basic block is executed.

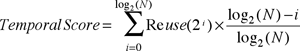
The choice of metric to use to capture temporal reuse is far from being widely accepted. A naïve approach relies on keeping track of every accessed address and determining upon a match the distance, in terms of the number of accesses, between repeating address locations. Use of this approach at the lowest level of instrumentation makes this an infeasible approach as suggested by Snavely et. al.,7 where the authors report application slowdowns in the range of 10x to 20x. This effectively limits the scope of the instrumentation and forces the implementation to rely on sampling techniques for feasibility.
Instead, we rely on high-level source code instrumentation and program analysis to reduce the number of array references that are instrumented. In our own experiments, we observed a slowdown in the order of 15% much lower than the slowdown reported by the lower-level instrumentation techniques. Specifically, we use the temporal scoring expression shown below as reported originally in Weinberg et. al.7 In this scoring, temporal locality is seen as a weighted sum of the fraction of the dynamic references that exhibit a reuse distance of 2i for decreasing weights with the increased reuse distance. The weight factor Weight(i) of (log2(N) – i)/log2(N) for references with a reuse distance of 2i gives a higher weight to references with a smaller reuse distances and much less to increasing reuse distances. The implementation simply keeps track of how many references do exhibit a reuse of increasingly larger values (as powers of 2) and keeps track of the number of memory references.
We now describe the utilization of the compiler analysis and code instrumentation infrastructure, described in the previous two sections, to several kernels codes, respectively, the CGM kernel from the NAS benchmark suite, a streaming kernel streamadd, and randomaccess from the HPCS benchmark suite. Whereas the spatial and temporal behavior of the HPCS kernels is fairly intuitive, the CGM kernel offers a mix of simple behaviors making it a richer example to experiment with.
The NAS CGM kernel is written in FORTRAN and implements the conjugate-gradient (CGM) iterative refinements method for a positive-definite input sparse-matrix. At the core of this kernel is the matvec subroutine that implements the sparse-matrix vector multiplication computation as depicted in the figure below.
735: subroutine matvec(n, a, rowidx, colstr, x, y)
736: c
737: integer rowidx(1), colstr(1)
738: integer n, i, j, k
739: real*8 a(1), x(n), y(n), xj
740: c
741: do 10 i = 1, n
742: y(i) = 0.0d0
743: 10 continue
744: do 200 j = 1, n
745: xj = x(j)
746:
747: do 100 k = colstr(j) , colstr(j+1)-1
748: y(rowidx(k)) = y(rowidx(k)) + a(k) * xj
749: 100 continue
750: 200 continue
751: return
752: end
The streamadd kernel is written in C and consists of a simple array vector addition loop. The length of the vector and thus of the manipulated arrays is fairly large, say 10,000 elements, to exercise the bandwidth of the memory subsystem. The randomaccess kernel, also known as the gups kernel, performs many updates to randomly selected locations in memory where the addresses of the locations are pre-computed in a loop before the updates take place. Figure 7 below depicts the relevant portions of the C source code for these kernels.
|
|
streamadd (left) and randomaccess (right) kernels.For each code, the analysis identifies the number of basic blocks and instruments the code to capture the corresponding frequency of execution. Table 1 below depicts the various results for the various kernels. Row two presents the number of basic blocks and row three the minimum, maximum and the average number of times one of these basic blocks executes. Row four presents the number and type of strides the static analysis determines whereas row five presents the corresponding spatial locality score. Row 6 shows the temporal locality score using the formulation presented in figure 4 above.
streamadd |
randomaccess |
NAS CGM |
|
| Number of Basic Blocks | 5 | 12 | 14 |
| Frequency of Execution [min, avg, max] | [1:200:1,000] | [1::2,000,000] | [1:269,729:1,853,104] |
| Stride and Reference Information | 3 refs stride 1 | 1 ref stride 0; 2 refs random | 2 refs random; 7 refs stride 1 |
| Spatial Score | 0.999 | 0.001 | 0.714 |
| Temporal Score | 0.1 | 0.000 | 0.422 |
Notice that the spatial score taking into account the frequency with which each basic block executes and thus although CGM has seven references with stride 1 in the various basic blocks of the core of this computation its spatial score is lower that the number of strided-1 references would otherwise suggest. This is due to the fact that some basic blocks with high spatial score execute very seldom.
The results presented here resulting from the combination of static and dynamic program behavior information are very encouraging. First, the spatial and temporal locality are qualitatively very close to the results for the same kernel codes as reported by Snavely et. al.,7 and are qualitatively identical. This is depicted by the black diamonds in figure 4. The basic difference for the random access kernel stems from the fact that in different implementations and with different compilers they do have slightly different methods to deal with table (array) accesses. Second, they rely on high-level instrumentation with much lower overheads making them feasible for instrumentation in larger scalar applications that can run to completion much more realistic runs that are possible today with low-level instrumentation approaches. Lastly, this approach allows us to derive much more accurate pictures of the behavior of the program without being cluttered or overwhelmed with the amount of data generated by low level approaches. For instance, using the approach described here we can determine why on the spatial or temporal locality, what they are and what are the dynamic references that contribute to the various metrics. Whereas low-level instrumentation approaches can also determine the source of the program behavior they lack the connection to the source code level this approach inherently preserves.
Understanding the behavior of program is a long-standing and sought-after goal. The traditional approach relies on low-level instrumentation techniques to extract performance or execution metrics that can indicate why the performance of a given program is what it is. The high overhead of this approach, the inherent Heissenberg effects of instrumentation and the sheer volume of generated data make it difficult to correlate program behavior with source code constructs. In this article we have described an integrated compiler and run-time approach that allows the extraction of relevant program behavior information by judiciously instrumenting the source code, and deriving performance metrics such as range of array reference addresses and stride and reuse distance information. We have illustrated the application of this approach in instrumenting several kernel codes for spatial and temporal locality scoring. For these kernel codes, this approach derives concrete values for these locality metrics that are qualitatively identical to the scoring obtained by low-level instrumentation of the code but at a much lower execution time cost. This suggests the approach to be extremely valuable in allowing large codes to execute in realistic settings.